
已知函数f(x)= sin 2x-cos2x-
sin 2x-cos2x- ,x∈R.
,x∈R.
(1)求函数f(x)的最小值和最小正周期;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且c=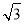 ,f(C)=0,若sin B=2sin A,求a,b的值.
,f(C)=0,若sin B=2sin A,求a,b的值.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源:2014高考名师推荐数学文科倾斜角与斜率(解析版) 题型:选择题
点M(x,y)在函数y=-2x+8的图象上,当x∈[2,5]时, 的取值范围是( )
的取值范围是( )
A.[- ,2] B.[0,
,2] B.[0, ]
]
C.[- ,
, ] D.[2,4]
] D.[2,4]
查看答案和解析>>
科目:高中数学 来源:2014高考名师推荐数学文科y=Asinwx+图像(解析版) 题型:选择题
已知函数 的图象由
的图象由 的图象向右平移
的图象向右平移 个单位得到,这两个函数的部分图象如图所示,则
个单位得到,这两个函数的部分图象如图所示,则 的值为( )
的值为( )

A. 
B. 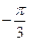
C. 
D. 
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(四)(解析版) 题型:选择题
如图所示,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A—BCD,则在三棱锥A—BCD中,下列命题正确的是( )

A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:解答题
已知函数f(x)=aln x-ax-3(a∈R).
(1)若a=-1,求函数f(x)的单调区间;
(2)若函数y=f(x)的图象在点(2,f(2))处的切线的倾斜角为45°,对于任意的t∈[1,2],函数g(x)=x3+x2 (f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(f′(x)是f(x)的导数)在区间(t,3)上总不是单调函数,求m的取值范围;
(3)求证: ×…×
×…× <
< (n≥2,n∈N*).
(n≥2,n∈N*).
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
设F1、F2分别是椭圆 (a>b>0)的左、右焦点,若在直线x=
(a>b>0)的左、右焦点,若在直线x= 上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
上存在P,使线段PF1的中垂线过点F2,则椭圆离心率的取值范围是( )
A. B.
B.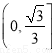 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(六)(解析版) 题型:选择题
设m、n是不同的直线,α、β是不同的平面,下列四个命题中正确的是( )
A.若m∥α,n∥α,则m∥n
B.若m⊥β,n⊥β,则m∥n
C.若α⊥β,m?α,则m⊥β
D.若m?α,n?α,m∥β,n∥β,则α∥β
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(五)(解析版) 题型:选择题
以双曲线 (a>0,b>0)的左焦点F为圆心,作半径为b的圆F,则圆F与双曲线的渐近线( )
(a>0,b>0)的左焦点F为圆心,作半径为b的圆F,则圆F与双曲线的渐近线( )
A.相交 B.相离 C.相切 D.不确定
查看答案和解析>>
科目:高中数学 来源:2014年高考数学考前复习冲刺穿插滚动练习(三)(解析版) 题型:选择题
已知函数y=f(x)是定义在R上且以3为周期的奇函数,当x∈ 时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
时,f(x)=ln(x2-x+1),则函数f(x)在区间[0,6]上的零点个数为( )
A.3 B.5 C.7 D.9
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com