练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    14．数列$\frac{1}{2}，\frac{1}{6}，\frac{1}{12}，\frac{1}{20}，…$的一个通项公式是（　　）
    A．${a_n}=\frac{1}{n（n-1）}$B．${a_n}=\frac{1}{2n（2n-1）}$C．${a_n}=\frac{1}{n}-\frac{1}{n+1}$D．${a_n}=1-\frac{1}{n}$

    分析 根据裂项和规律即可得到数列的通项公式

    解答 解：数列$\frac{1}{2}，\frac{1}{6}，\frac{1}{12}，\frac{1}{20}，…$的一个通项公式是$\frac{1}{1×2}$，$\frac{1}{2×3}$，$\frac{1}{3×4}$，$\frac{1}{4×5}$，…，即为（1-$\frac{1}{2}$），（$\frac{1}{2}$-$\frac{1}{3}$），（$\frac{1}{3}$-$\frac{1}{4}$），（$\frac{1}{4}$-$\frac{1}{5}$），…，
    ∴an=$\frac{1}{n}$-$\frac{1}{n+1}$，
    故选：C

    点评 本题考查数列的通项公式，考查学生分析解决问题的能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

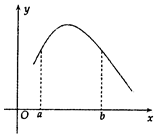    4．函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（　　）
    A．$f'（{\frac{2ab}{a+b}}）＜f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）$B．$f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{a+b}{2}}）$
    C．$f'（{\frac{a+b}{2}}）＜f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）$D．$f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{2ab}{a+b}}）$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    5．有一段演绎推理是这样的：“直线平行于平面，则此直线平行于平面内的所有直线；已知直线b∥平面α，直线a?平面α，则直线b∥直线a”．结论显然是错误的，这是因为（1）．
    （1）大前提错误    （2）推理形式错误     （3）小前提错误     （4）以上都错误．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．已知数列{an}的前n项和为Sn，a1=1且an+1=2Sn+1（n∈N*）；
    数列{bn}中，b1=3且对n∈N*，点（bn，bn+1）都在函数y=x+2的图象上．
    （Ⅰ）求数列{an}，{bn}的通项公式；
    （Ⅱ）是否存在正整数n，使得a1b1+a2b2+…+anbn＞100n？若存在，求n的最小值；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    9．（1）已知关于x的不等式ax2+bx+c＜0的解集是{x|x＜-2，或x＞-$\frac{1}{2}$}，求不等式ax2-bx+c＞0的解集．
    （2）已知M是关于x的不等式2x2+（3a-7）x+3+a-2a2＜0的解集，且M中的一个元素是0，求实数a的取值范围，并用a表示出该不等式的解集．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    19．（1）已知椭圆方程为$\frac{x^2}{4}+\frac{y^2}{3}$=1，点$P（0，\sqrt{3}）$．
    i．若关于原点对称的两点A1（-2，0），B1（2，0），记直线PA1，PB1的斜率分别为${k_{P{A_1}}}，{k_{P{B_1}}}$，试计算${k_{P{A_1}}}•{k_{P{B_1}}}$的值；
    ii．若关于原点对称的两点${A_2}（\sqrt{3}，\frac{{\sqrt{3}}}{2}），{B_2}（-\sqrt{3}，-\frac{{\sqrt{3}}}{2}）$，记直线PA2，PB2的斜率分别为${k_{P{A_2}}}，{k_{P{B_2}}}$，试计算${k_{P{A_2}}}•{k_{P{B_2}}}$的值；
    （2）根据上题结论探究：若M，N是椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）上关于原点对称的两点，点Q是椭圆上任意一点，且直线QM，QN的斜率都存在，并分别记为kQM，kQN，试猜想kQM•kQN的值，并加以证明．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    6．已知等差数列{an}的前n和为Sn，公差d≠0．且a3+S5=42，a1，a4，a13成等比数列
    （Ⅰ）求数列{an}的通项公式；
    （Ⅱ）若Sn表示数列{an}的前n项和，求数列$\left\{{\frac{1}{S_n}}\right\}$的前n项和Tn．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    3．若tanα=4的值，则$\frac{{sin（π-α）-sin（\frac{π}{2}+α）}}{cos（-α）}$=3．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    10．求下列函数的导数
    （1））y=$\root{4}{{x}^{3}}$+2x+5；              
    （2）y=x2sinx+cosx．

    查看答案和解析>>

    同步练习册答案