
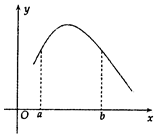
 函数f(x)的图象如图所示,设f'(x)是f(x)的导函数,若0<a<b,下列各式成立的是( )
函数f(x)的图象如图所示,设f'(x)是f(x)的导函数,若0<a<b,下列各式成立的是( )| A. | $f'({\frac{2ab}{a+b}})<f'({\frac{a+b}{2}})<f'({\sqrt{ab}})$ | B. | $f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})<f'({\frac{a+b}{2}})$ | ||
| C. | $f'({\frac{a+b}{2}})<f'({\frac{2ab}{a+b}})<f'({\sqrt{ab}})$ | D. | $f'({\frac{a+b}{2}})<f'({\sqrt{ab}})<f'({\frac{2ab}{a+b}})$ |
分析 由基本不等式可得$\frac{2ab}{a+b}<\sqrt{ab}<\frac{a+b}{2}$,再由函数f(x)的图象得到f'(x)的单调性,则答案可求.
解答 解:∵b>a>0,
∴$\frac{a+b}{2}>\sqrt{ab}$>0,
则$\frac{1}{\sqrt{ab}}>\frac{2}{a+b}$,两边同时乘以ab,得$\frac{ab}{\sqrt{ab}}>\frac{2ab}{a+b}$,即$\sqrt{ab}>\frac{2ab}{a+b}$.
∴$\frac{2ab}{a+b}<\sqrt{ab}<\frac{a+b}{2}$.
∵函数f(x)的图象是上凸型,由导数的几何意义可知,f′(x)为定义域上的减函数,
则$f'({\frac{a+b}{2}})<f'({\sqrt{ab}})<f'({\frac{2ab}{a+b}})$.
故选:D.
点评 本题考查利用导数研究函数的单调性,考查导数的几何意义,训练了利用基本不等式进行大小比较,属中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
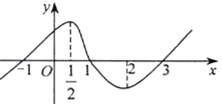 已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x-1)f′(x)<0的解集为(-∞,$\frac{1}{2}$)∪(1,2).
已知函数y=f(x)(x∈R)的图象如图所示,f′(x)是f(x)的导函数,则不等式(x-1)f′(x)<0的解集为(-∞,$\frac{1}{2}$)∪(1,2).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{7}$ | B. | $\frac{1}{7}$ | C. | $-\frac{1}{6}$ | D. | $\frac{1}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,2] | B. | [1,2] | C. | (0,2] | D. | ($\frac{\sqrt{3}}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{1}{n(n-1)}$ | B. | ${a_n}=\frac{1}{2n(2n-1)}$ | C. | ${a_n}=\frac{1}{n}-\frac{1}{n+1}$ | D. | ${a_n}=1-\frac{1}{n}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com