
分析 (Ⅰ)由an+1=2Sn+1(n∈N*),an=2Sn-1+1(n∈N*)得an+1-an=2a_n,}an+1=3an,即$\frac{{a}_{n+1}}{{a}_{n}}=3,(n≥2)$
由点(bn,bn+1)都在函数y=x+2的图象上.得数列 {bn}是公差为2的等差数列
(Ⅱ)设数列{an•bn}的前n项和为Tn,an•bn=(2n+1)3n-1
利用错位相减法求得Tn,由题意n•3n>100,得n≥5
解答 解:(Ⅰ)当n=1时,a2=2s1+1=3…(1分)
且an+1=2Sn+1(n∈N*); ①
∴当n≥2时,an=2Sn-1+1(n∈N*); ②…(2分)
①-②得an+1-an=2a_n,}an+1=3an
即$\frac{{a}_{n+1}}{{a}_{n}}=3,(n≥2)$
又当n=1时,$\frac{{a}_{2}}{{a}_{1}}=3$也符合$\frac{{a}_{n+1}}{{a}_{n}}=3$
所以数列{an}是首项为1,公比为3的等比数列,${a}_{n}={3}^{n-1}$…(4分)
∵点(bn,bn+1)都在函数y=x+2的图象上∴bn+1=bn+2,bn+1-bn=2.
所以数列 {bn}是公差为2的等差数列,
bn=3+(n-1)×2=2n+1…(6分)
(Ⅱ)设数列{an•bn}的前n项和为Tn,∵an•bn=(2n+1)3n-1…(7分)
∴Tn=3•30+5•31+7•32+…+(2n-1)•3n-2+(2n+1)•3n-1…①
3Tn=3•31+5•32+7•33+…+(2n-1)3n-1+(2n+1)3n…②…(8分)
①-②得:-2Tn=3+2(31+32+33+…+3n-1)-(2n-1)•3n=-2n•3n
∴${T}_{n}=n•{3}^{n}$…(10分)
由题意n•3n>100n,即3n>100,∴n≥5
使得a1b1+a2b2+…+anbn>100n?若存在,n的最小值为5,…(12分)
点评 本题考查了数列的递推式,数列的通项公式,考查了错位相减法求和,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | ($\sqrt{3}$,2] | B. | [1,2] | C. | (0,2] | D. | ($\frac{\sqrt{3}}{2}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{2}{3}$π | C. | $\frac{4}{3}$π | D. | $\frac{5}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$) | C. | [-3,-1)∪(1,3] | D. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{1}{n(n-1)}$ | B. | ${a_n}=\frac{1}{2n(2n-1)}$ | C. | ${a_n}=\frac{1}{n}-\frac{1}{n+1}$ | D. | ${a_n}=1-\frac{1}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
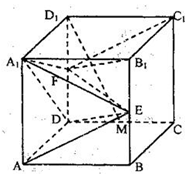 在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.
在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1<a<2 | B. | -3<a<6 | C. | a<-3或a>6 | D. | a<-1或a>2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com