
分析 (1)i.求出直线PA1,PB1的斜率分别为${k_{P{A_1}}},{k_{P{B_1}}}$,计算${k_{P{A_1}}}•{k_{P{B_1}}}$求解即可.
ii.求解直线PA2,PB2的斜率分别为${k_{P{A_2}}},{k_{P{B_2}}}$,然后求解${k_{P{A_2}}}•{k_{P{B_2}}}$的值即可.
(2)猜想${k_{QM}}•{k_{QN}}=-\frac{b^2}{a^2}$,设点M(m,n),则点N(-m,-n),从而$\frac{m^2}{a^2}+\frac{n^2}{b^2}=1$,设点Q(x,y),求出斜率,然后代入化简求解即可.
解答 解:(1)i.因为${k_{P{A_1}}}=\frac{{\sqrt{3}-0}}{0+2}=\frac{{\sqrt{3}}}{2},{k_{P{B_1}}}=\frac{{\sqrt{3}-0}}{0-2}=-\frac{{\sqrt{3}}}{2}$,
所以${k_{P{A_1}}}•{k_{P{B_1}}}=\frac{{\sqrt{3}}}{2}×(-\frac{{\sqrt{3}}}{2})=-\frac{3}{4}$….(3分)
ii.因为${k_{P{A_2}}}=\frac{{\sqrt{3}-\frac{{\sqrt{3}}}{2}}}{{0-\sqrt{3}}}=-\frac{1}{2},{k_{P{B_2}}}=\frac{{\sqrt{3}+\frac{{\sqrt{3}}}{2}}}{{0+\sqrt{3}}}=\frac{3}{2}$,
所以${k_{P{A_2}}}•{k_{P{B_2}}}=-\frac{1}{2}×\frac{3}{2}=-\frac{3}{4}$…..(6分)
(2)猜想${k_{QM}}•{k_{QN}}=-\frac{b^2}{a^2}$…..…(8分)
证明:设点M(m,n),则点N(-m,-n),从而$\frac{m^2}{a^2}+\frac{n^2}{b^2}=1$,设点Q(x,y),
由${k_{QM}}=\frac{y-n}{x-m},{k_{QN}}=\frac{y+n}{x+m}$,…(10分)
得${k_{QM}}•{k_{QN}}=\frac{y-n}{x-m}•\frac{y+n}{x+m}=\frac{{{y^2}-{n^2}}}{{{x^2}-{m^2}}}$,(*)
由${y^2}={b^2}-\frac{{{b^2}{x^2}}}{a^2}$,${n^2}={b^2}-\frac{{{b^2}{m^2}}}{a^2}$,…..…(12分)
代入(*)式得${k_{QM}}•{k_{QN}}=\frac{{{b^2}-\frac{{{b^2}{x^2}}}{a^2}-{b^2}+\frac{{{b^2}{m^2}}}{a^2}}}{{{x^2}-{m^2}}}=\frac{{{b^2}({m^2}-{x^2})}}{{{a^2}({x^2}-{m^2})}}=-\frac{b^2}{a^2}$
所以${k_{QM}}•{k_{QN}}=-\frac{b^2}{a^2}$…(16分)
点评 本题考查直线与椭圆的位置关系的综合应用,考查转化思想以及计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\sqrt{3}$,$\sqrt{3}$] | B. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$) | C. | [-3,-1)∪(1,3] | D. | [-$\sqrt{3}$,-$\sqrt{2}$)∪($\sqrt{2}$,$\sqrt{3}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ${a_n}=\frac{1}{n(n-1)}$ | B. | ${a_n}=\frac{1}{2n(2n-1)}$ | C. | ${a_n}=\frac{1}{n}-\frac{1}{n+1}$ | D. | ${a_n}=1-\frac{1}{n}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
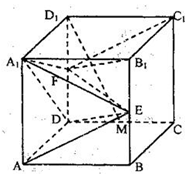 在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.
在正方体ABCD-A1B1C1D1中,E、F分别为棱BB1和DD1的中点,M为棱DC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 大前提 | B. | 小前提 | C. | 结论 | D. | 无错误 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com