Question

7．某几何体的三视图如图所示，则该几何体的表面积等于（　　）

• A． 8+2$\sqrt{2}$
• B． 11+2$\sqrt{2}$
• C． 14+2$\sqrt{2}$
• D． 15

Answer 1

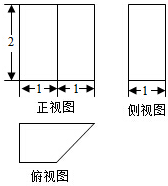
分析 判断出该几何体是底面为直角梯形，高为2的直四棱柱，底面的梯形上底1，下底2，高为1，运用梯形，矩形的面积公式求解即可．

解答 解：根据三视图可判断该几何体是底面为直角梯形，高为2的直四棱柱，
底面的梯形上底1，下底2，高为1，
∴侧面为（4$+\sqrt{2}$）×2=8$+2\sqrt{2}$，
底面为$\frac{1}{2}×$（2+1）×1=$\frac{3}{2}$，
故几何体的表面积为8$+2\sqrt{2}$$+2×\frac{3}{2}$=11$+2\sqrt{2}$，
故选：B．

点评 本题考查了空间几何体的三视图的运用，空间想象能力，关键是能够恢复判断几何体的形状．