
分析 (Ⅰ)求出f′(x)=(x-1)ex-ax,假设函数f(x)的图象与x轴相切于点(t,0),则$\left\{\begin{array}{l}{f(t)=0}\\{{f}^{'}(t)=0}\end{array}\right.$,从而t2-3t+4=0,由根的判别式得方程t2-3t+4=0无解,由此得到无论a取何值,函数f(x)的图象都不与x轴相切.
(Ⅱ)记g(x)=(x-2)ex-$\frac{a}{2}{x}^{2}$+2≥0在R上恒成立,由g′(1)=-a+2≥0,得g′(x)≥0的必要条件是a≤2,当a=1时,不等式(x-1)ex-x+2≥0恒成立.由此利用导数性质能求出a能取得的最大整数.
解答 解:(Ⅰ)∵f(x)=(x-2)ex-$\frac{a}{2}$x2,
∴f′(x)=(x-1)ex-ax,
假设函数f(x)的图象与x轴相切于点(t,0),
则有:$\left\{\begin{array}{l}{f(t)=0}\\{{f}^{'}(t)=0}\end{array}\right.$,即$\left\{\begin{array}{l}{(t-2){e}^{t}-\frac{a}{2}{t}^{2}=0,①}\\{(t-1){e}^{t}-at=0,②}\end{array}\right.$,
由②知at=(t-1)et,代入①中,得(t-2)et-$\frac{t(t-1)}{2}{e}^{t}$=0,
∵et>0,∴(t-2)-$\frac{t(t-1)}{2}$=0,即t2-3t+4=0,
∵△=9-16=-7<0,
∴方程t2-3t+4=0无解,
∴无论a取何值,函数f(x)的图象都不与x轴相切.
(Ⅱ)记g(x)=(x-2)ex-$\frac{a}{2}{x}^{2}$+2≥0在R上恒成立,
由g′(1)=-a+2≥0,得g′(x)≥0的必要条件是a≤2,
若a=2,则g′(x)=(x-1)ex-2x+2=(x-1)(ex-2),
当ln2<x<1时,g′(x)<0,故a<2.
下面证明:当a=1时,不等式(x-1)ex-x+2≥0恒成立.
令h(x)=(x-1)ex-x+2,则h′(x)=xex-1,
记H(x)=xex-1,则H′(x)=(x+1)ex,
当x>-1时,H′(x)>0,H(x)单调递增且H(x)>-$\frac{1}{e}-1$,
当x<-1时,H′(x)<0,H(x)单调递减,且-$\frac{1}{e}-1<$H(x)<0,
∵H($\frac{1}{2}$)=$\frac{\sqrt{e}}{2}$-1<0,H(1)=e-1>0,
∴存在唯一的${x}_{0}∈(\frac{1}{2},1)$,使得H(x0)=0,且当x∈(-∞,x0)时,H(x)>0,
h(x)单调递减,
当x∈(x0,+∞)时,H(x)<0,h(x)单调递增,
∴h(x)min=h(x0)=(x0-1)${e}^{{x}_{0}}$-x0+2,
∵H(x0)=0,∴${e}^{{x}_{0}}=\frac{1}{{x}_{0}}$,
∴h(x0)=(x0-1)$\frac{1}{{x}_{0}}-{x}_{0}+2$=3-($\frac{1}{{x}_{0}}+{x}_{0}$),
∵$\frac{1}{2}<{x}_{0}<1$,∴2<$\frac{1}{{x}_{0}}+{x}_{0}$<$\frac{5}{2}$,
∴h(x)min=h(x0)>0,
∴(x-1)ex-x-2≥0恒成立,
∴a能取得的最大整数为1.
点评 本题考查导数及其应用、不等式、函数等基础知识,考查考查推理论证能力、运算求解能力、抽象概括能力,考查化归与转化思想、函数与方程思想、分类与整合思想,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
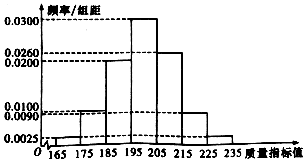 某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:
某种产品的质量以其质量指标衡量,并依据质量指标值划分等级如表:| 质量指标值m | m<185 | 185≤m<205 | M≥205 |
| 等级 | 三等品 | 二等品 | 一等品 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
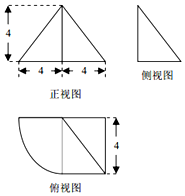
| A. | $\frac{16}{3}$π | B. | $\frac{64}{3}$ | C. | $\frac{16π+64}{3}$ | D. | 16π+64 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2016}$ | B. | $\frac{1}{2017}$ | C. | $\frac{1}{2018}$ | D. | $\frac{1}{2019}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 150° | B. | 60° | C. | 120° | D. | 30° |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com