
各项均不为零的数列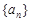 的前
的前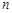 项和为
项和为 ,且
,且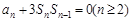 ,
,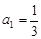 .
.
(1)求数列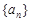 的通项公式
的通项公式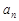 ;
;
(2)若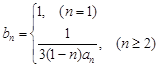 ,设
,设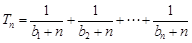 ,若
,若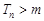 对
对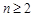 恒成立,求实数
恒成立,求实数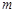 的取值范围.
的取值范围.
(1)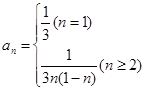 ;(2)
;(2)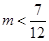 .
.
解析试题分析:(1)考虑到当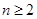 时,有
时,有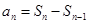 ,因此可由条件中的关系式
,因此可由条件中的关系式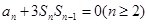 首先得到
首先得到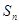 ,
,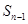 的关系式,通过求得数列
的关系式,通过求得数列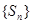 的通项公式进而求得
的通项公式进而求得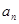 :由
:由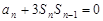 可得
可得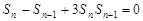 ,即
,即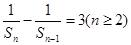 ,又∵
,又∵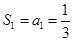 ,∴数列
,∴数列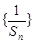 是以
是以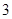 为首项,以
为首项,以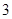 为公差的等差数列,∴
为公差的等差数列,∴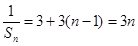 ,∴
,∴ ,∴
,∴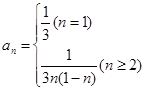 ;(2)由(1)可知,
;(2)由(1)可知,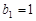 ,
,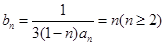 ,故可求得
,故可求得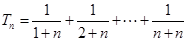 ,而要使
,而要使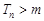 对
对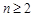 恒成立,等价于当
恒成立,等价于当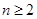 时,求数列
时,求数列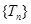 的最小项,因此考虑通过考查数列
的最小项,因此考虑通过考查数列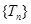 的单调性来求其最小项:
的单调性来求其最小项: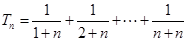 ,
,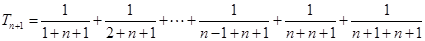 ,
,
∴ ,即
,即 为单调递增,∴当
为单调递增,∴当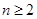 时,
时,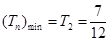 ,因此只需
,因此只需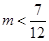 .
.
试题解析:(1)当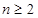 时,由
时,由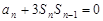 可得
可得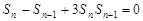 ,
,
即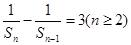 , 2分
, 2分
又∵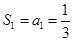 ,∴数列
,∴数列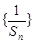 是以
是以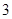 为首项,以
为首项,以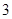 为公差的等差数列,
为公差的等差数列,
∴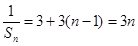 ,∴
,∴ , 4分
, 4分
当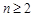 时,
时, ,∴
,∴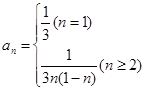 ; 6分
; 6分
(2)∵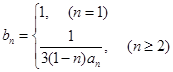 ,∴
,∴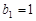 ,
,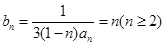
∴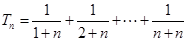 ,
,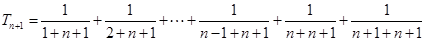 ,
,
∴ ,∴
,∴ 为单调递增, 10分
为单调递增, 10分
∴当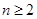 时,
时,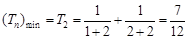 ,∴要使
,∴要使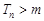 对
对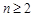 恒成立,只需
恒成立,只需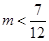 . 12分
. 12分
考点:1.数列的通项公式;2.数列的单调性判断.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com