
分析 (Ⅰ)通过直线OP,OQ互相垂直,以及点的坐标适合椭圆方程,求出圆的圆心,然后求圆R的方程;
(Ⅱ)当直线OP,OQ斜率k1、k2都存在时,推导出k1,k2是方程(x02-4)k2-2x0y0k+y02-4=0的两个不相等的实数根,由此利用达定理结合已知条件得到x0=$\sqrt{19}$,${{y}_{0}}^{2}=\frac{1}{2}-\frac{19}{2}$=-9不成立,从而得到不存在点R,当直线OP,OQ斜率k1、k2都存在时,使得k1k2-$\frac{{k}_{1}+{k}_{2}}{{x}_{0}{y}_{0}}$+1=0.
解答 解:(Ⅰ)由题意圆的半径为2,
∵OP⊥OQ,且OP、OQ都与圆相切,
∴OR=$\sqrt{4+4}$=2$\sqrt{2}$,∴${{x}_{0}}^{2}+{{y}_{0}}^{2}$=8,①
∵点R(x0,y0)在椭圆C上,∴$\frac{{{x}_{0}}^{2}}{12}+\frac{{{y}_{0}}^{2}}{6}=1$,②
由①②及R在第一象限,解得x0=y0=2,
∴圆R的方程为:(x-2)2+(y-2)2=4.
(Ⅱ)不存在点R,当直线OP,OQ斜率k1、k2都存在时,使得k1k2-$\frac{{k}_{1}+{k}_{2}}{{x}_{0}{y}_{0}}$+1=0.
理由如下:
∵当直线OP,OQ斜率k1、k2都存在时,从原点O向圆R:(x-x0)2+(y-y0)2=4作两条切线,切点分别为P、Q,
∴直线OP:y=k1x,直线OQ:y=k2x均于圆R相切,
∵直线OP:y=k1x,OQ:y=k2x,与圆R相切,
∴$\left\{\begin{array}{l}{y={k}_{1}x}\\{(x-{x}_{0})^{2}+(y-{{y}_{0})}^{2}=4}\end{array}\right.$,化简得(1+${{k}_{1}}^{2}$)x2-(2x0+2k1y0)x+${{x}_{0}}^{2}+{{y}_{0}}^{2}$-4=0,
同理$(1+{{k}_{2}}^{2}){x}^{2}-(2{x}_{0}+2{k}_{2}{y}_{0})x+{{x}_{0}}^{2}+{{y}_{0}}^{2}-4=0$,
∴k1,k2是方程(x02-4)k2-2x0y0k+y02-4=0的两个不相等的实数根,
∴k1k2=$\frac{-b+\sqrt{{b}^{2}-4ac}}{2a}$•$\frac{-b-\sqrt{{b}^{2}-4ac}}{2a}$=$\frac{c}{a}$=$\frac{{{y}_{0}}^{2}-4}{{{x}_{0}}^{2}-4}$,k1+k2=$\frac{2{x}_{0}{y}_{0}}{{{x}_{0}}^{2}-4}$,
∵点R(x0,y0)在椭圆C上,∴$\frac{{{x}_{0}}^{2}}{12}+\frac{{{y}_{0}}^{2}}{6}=1$,
即${{y}_{0}}^{2}$=$\frac{1}{2}-\frac{{{x}_{0}}^{2}}{2}$,
∴k1k2-$\frac{{k}_{1}+{k}_{2}}{{x}_{0}{y}_{0}}$+1=$\frac{{{y}_{0}}^{2}-4}{{{x}_{0}}^{2}-4}$-$\frac{2}{{{x}_{0}}^{2}-4}$+1=$\frac{{{x}_{0}}^{2}+{{y}_{0}}^{2}-10}{{{x}_{0}}^{2}-4}$=$\frac{\frac{{{x}_{0}}^{2}}{2}-\frac{19}{2}}{{{x}_{0}}^{2}-4}$=0,
解得x0=$\sqrt{19}$,${{y}_{0}}^{2}=\frac{1}{2}-\frac{19}{2}$=-9不成立,
故不存在点R,当直线OP,OQ斜率k1、k2都存在时,使得k1k2-$\frac{{k}_{1}+{k}_{2}}{{x}_{0}{y}_{0}}$+1=0.
点评 本题考查直线与椭圆的综合应用,直线与圆相切关系的应用,考查分析问题解决问题的能力.转化思想的应用.


 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$ | B. | $\frac{{x}^{2}}{12}+\frac{{y}^{2}}{9}=1$ | C. | $\frac{{x}^{2}}{5}+\frac{{y}^{2}}{3}=1$ | D. | $\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
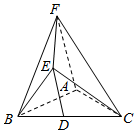 在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.
在如图所示的几何体EFABC中,已知△ABC是等腰三角形,AB=AC,AF⊥平面ABC,D为BC的中点,DE∥AF且BC=AF=2DE=2.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{3}{4}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com