
| A. | b2<c<a2 | B. | ab+$\frac{1}{ab}$<c | C. | $\frac{1}{b}$<$\frac{1}{a}$<$\frac{1}{c}$ | D. | b2>ab-bc+ac |
分析 可通过举反例的方法说明选项A,B错误,而由不等式的性质及条件便可判断出选项C正确,通过作差,分解因式及条件便可判断出b2和ab-bc+ac的关系不确定,即选项D错误.
解答 解:A错误,比如b=$-\frac{1}{2}$,$c=\frac{1}{5}$时,不满足b2<c;
B错误,比如$a=-100,b=-\frac{1}{2},c=\frac{1}{2}$时,不满足$ab+\frac{1}{ab}<c$;
C正确,a<b<0,∴$\frac{1}{b}<\frac{1}{a}<0$;
又$\frac{1}{c}>0$;
∴$\frac{1}{b}<\frac{1}{a}<\frac{1}{c}$;
D错误,b2-(ab-bc+ac)=(b2-ab)+(bc-ac)=(b-a)(b+c);
∵a<b;
∴b-a>0;
又-1<b<0<c<1;
∴b+c的符号不确定;
∴不能判断b2和ab-bc+ac的关系.
故选:C.
点评 考查通过举反例的方法说明选项错误,以及不等式的性质,作差法比较两个式子的大小.


科目:高中数学 来源: 题型:选择题
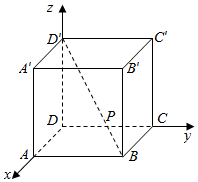
| A. | ($\frac{1}{3}$$,\frac{1}{3}$,$\frac{1}{3}$) | B. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{2}{3}$) | C. | ($\frac{5}{6}$,$\frac{5}{6}$,$\frac{1}{6}$) | D. | ($\frac{2}{3}$,$\frac{2}{3}$,$\frac{1}{3}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
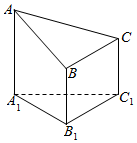 如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体,截面为△ABC,已知AA1=4,BB1=2,CC1=3,在边AB上是否存在一点O,使得OC∥平面A1B1C1?
如图是一个以△A1B1C1为底面的直角三棱柱被一平面截得的几何体,截面为△ABC,已知AA1=4,BB1=2,CC1=3,在边AB上是否存在一点O,使得OC∥平面A1B1C1?查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③④ | C. | ①③ | D. | ②④ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com