
分析 构造向量$\overrightarrow{a}$=( 1-cosβ,sinβ),$\overrightarrow{b}$=(cosα,sinα),则可求$\overrightarrow{a}$•$\overrightarrow{b}$,|$\overrightarrow{a}$|2•|$\overrightarrow{b}$|2,由($\overrightarrow{a}$•$\overrightarrow{b}$)22≤|$\overrightarrow{a}$|2•|$\overrightarrow{b}$|2,整理得 (cosβ-$\frac{1}{2}$)2≤0,解得cosβ,结合范围即可得解.
解答 解:原等式化为( 1-cosβ)cosα+sinβsinα=$\frac{3}{2}$-cosβ ①
构造向量$\overrightarrow{a}$=( 1-cosβ,sinβ),$\overrightarrow{b}$=(cosα,sinα),
则$\overrightarrow{a}$•$\overrightarrow{b}$=( 1-cosβ)cosα+sinβsinα=$\frac{3}{2}$-cosβ,
|$\overrightarrow{a}$|2•|$\overrightarrow{b}$|2=[(1-cosβ)2+sin2β]•[cos2α+sin2α]=2-2cosβ,
因 ($\overrightarrow{a}$•$\overrightarrow{b}$)22≤|$\overrightarrow{a}$|2•|$\overrightarrow{b}$|2,
于是有 ($\frac{3}{2}$-cosβ)2≤2-2cosβ,
整理得 (cosβ-$\frac{1}{2}$)2≤0,
∴cosβ=$\frac{1}{2}$.
又 β∈(0,π),
∴β=$\frac{π}{3}$.
同理可得α=$\frac{π}{3}$.
点评 对于某些三角问题,若能合理地构造向量,利用向量来解,往往可使问题得到快捷方便地解决,本题主要考查了平面向量及应用,三角函数恒等变换的应用,属于难题.


 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,1) | B. | [-1,1] | C. | (-∞,-1)∪(1,+∞) | D. | (-∞,-1]∪[1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )
把一个底面边长和高都为6的正三棱锥(底面是正三角形,从顶点向底面作垂线,垂足是底面的中心的三棱锥)P-ABC的底面ABC放置在平面α上,现让三棱锥绕棱BC逆时针方向旋转,使侧面PBC落在α内,则在旋转过程中正三棱锥P-ABC在α上的正投影图的面积取值范围是( )| A. | [$\frac{54\sqrt{13}}{13}$,12$\sqrt{3}$] | B. | [$\frac{54\sqrt{13}}{13}$,9$\sqrt{3}$] | C. | [$\frac{48\sqrt{13}}{13}$,12$\sqrt{3}$] | D. | [$\frac{48\sqrt{13}}{13}$,3$\sqrt{39}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
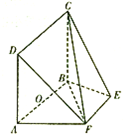 如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.
如图,等腰梯形ABEF中,AB∥EF,AB=2,AD=AF=1,AF⊥BF,O为AB的中点,矩形ABCD所在平面与平面ABEF互相垂直.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com