
����Ŀ�������ʱ��г���ǿ�ƽ��룬��������������������һҹ�����������鲼��һ���߳��еĴ��С��.Ϊ�˽��������![]() �е�ʹ�������ij���������������������ʾ����飬���Ӳ������������г�ȡ��200�˽��г����������õ�������λ���ˣ�
�е�ʹ�������ij���������������������ʾ����飬���Ӳ������������г�ȡ��200�˽��г����������õ�������λ���ˣ�
����ʹ�� | ż������ | �ϼ� | |
30�꼰���� | 70 | 30 | 100 |
30������ | 60 | 40 | 100 |
�ϼ� | 130 | 70 | 200 |
��1�������������ݣ��ܷ��ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������йأ�
��ʹ�ù�����������������йأ�
��2���ִ�����ȡ��30�����ϵ����������÷ֲ�����ķ����ٳ�ȡ5��.
��i���ֱ�����5���о���ʹ�á�ż�����ù���������������
��ii������5���У������ѡ��2������һ����Ʒ����ѡ����2����������1�˾���ʹ�ù��������ĸ���.
�ο���ʽ�� 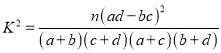 ������
������![]() .
.
�ο����ݣ�
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 3.841 | 5.024 | 6.635 |
���𰸡�(1)���ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������йأ�
��ʹ�ù�����������������йأ�
(2)(i)����ʹ�ù�����������3�ˣ�ż�����ù�����������2��.(ii) ![]()
�����������������
(1)���������ɵ�![]() ���������ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ
���������ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������й�.
��ʹ�ù�����������������й�.
(2)��i���������֪������ʹ�ù�����������![]() ���ˣ���ż�����ù�����������
���ˣ���ż�����ù�����������![]() ���ˣ�.
���ˣ�.
��ii���������г����п��ܵĽ������Ϲŵ����ʽ�Ͷ����¼���ʽ�ɵ�ѡ����2����������1�˾���ʹ�ù��������ĸ���![]() .
.
���������
��1������������֪��
![]() .
.
��Ϊ![]() ��
��
�������ڷ�����ĸ��ʲ�����0.15��ǰ������Ϊ![]() ��ʹ�ù�����������������й�.
��ʹ�ù�����������������й�.
��2����i���������֪������ȡ��5��30�����ϵ������У�����ʹ�ù�����������![]() ���ˣ���ż�����ù�����������
���ˣ���ż�����ù�����������![]() ���ˣ�.
���ˣ�.
��ii������5���У�����ʹ�ù���������3�˷ֱ�Ϊ![]() ��
�� ![]() ��
�� ![]() ��ż�����ù���������2�˷ֱ�Ϊ
��ż�����ù���������2�˷ֱ�Ϊ![]() ��
�� ![]() .
.
���5����ѡ��2�˵����п��ܽ��Ϊ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��10��.
��10��.
����û��1�˾���ʹ�ù��������Ŀ��ܽ��Ϊ![]() ��1�֣�
��1�֣�
��ѡ����2����������1�˾���ʹ�ù��������ĸ���![]() .
.


 ���ݼ���ϵ�д�
���ݼ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���![]() ������ʵ��
������ʵ��![]() �IJ���ʽ
�IJ���ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��
��1����![]() ʱ�������
ʱ�������![]() �IJ���ʽ��
�IJ���ʽ��![]() ��
��
��2���Ƿ����ʵ��![]() ��ʹ�ù���
��ʹ�ù���![]() �ĺ���
���![]() ��
��![]() ������СֵΪ
������СֵΪ![]() ������������ʵ��
������������ʵ��![]() ��ֵ���������ڣ�˵�����ɣ�
��ֵ���������ڣ�˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������R�ϵ��溯��f��x������x��0ʱ��f��x��=��x2+2x ��������f��x����R�ϵĽ���ʽ��
����������f��x��������[��1��a��2]�ϵ�����������ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���� ![]()
��1������f��x���� ![]() �ϵ����ֵ����Сֵ��
�ϵ����ֵ����Сֵ��
��2����֪ ![]() ��x0�ʣ�
��x0�ʣ� ![]() ��
�� ![]() ������cos4x0��ֵ��
������cos4x0��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���佫10������ƽ���ֳɼס�������ӹ�ij��������ڵ�λʱ����ÿ�������ӹ��ĺϸ��������ͳ�����ݵľ�Ҷͼ��ͼ��ʾ����֪���鼼���ڵ�λʱ���ڼӹ��ĺϸ����ƽ������Ϊ9�� 
��1���ֱ����m��n��ֵ��
��2���ֱ�����ס������鼼���ڵ�λʱ���ڼӹ��ĺϸ�����ķ��� ![]() ��
�� ![]() �����ɴ˷������鼼���ļӹ�ˮƽ��
�����ɴ˷������鼼���ļӹ�ˮƽ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
�� ![]()
![]() .
.
��1������![]() �ĵ������䣻
�ĵ������䣻
��2��������![]() �ķ���
�ķ���![]() ��ʵ��������ʵ��
��ʵ��������ʵ��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����f��x��=x3+3x2��9x+m
��1������f��x��=x3+3x2��9x+m�ĵ����������䣻
��2��������f��x��������[0��2]�ϵ����ֵ12������f��x���ڸ������ϵ���Сֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��l��P��1��2������A��2��3����B��4����5����l�ľ�����ȣ���ֱ��l�ķ����ǣ� ��
A.4x+y��6=0
B.x+4y��6=0
C.3x+2y��7=0��4x+y��6=0
D.2x+3y��7=0��x+4y��6=0
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������f��x��y��=0����y=f��x������������ͬ�㴦�������غϣ������������Ϊ����f��x��y��=0��y=f��x���ġ��Թ����ߡ������з��̣�
��x2��y2=1��
��y=x2��|x|��
��y=3sinx+4cosx��
��|x|+1= ![]()
��Ӧ�������д��ڡ��Թ����ߡ����У� ��
A.�٢�
B.�٢�
C.�ڢ�
D.�ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com