Question

17．已知向量$\overrightarrow{a}$与$\overrightarrow{b}$满足：|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，（2$\overrightarrow{a}$-3$\overrightarrow{b}$）•（2$\overrightarrow{a}$+$\overrightarrow{b}$）=61；
（1）求向量$\overrightarrow{a}$+$\overrightarrow{b}$的模；
（2）若$\overrightarrow{AB}$=$\overrightarrow{a}$，$\overrightarrow{AC}$=$\overrightarrow{b}$，作三角形ABC，点P是三角形ABC所在平面上任意一点，求（$\overrightarrow{PC}$+$\overrightarrow{PB}$）•$\overrightarrow{PA}$的最小值．

Answer 1

分析 （1）利用向量数量积的运算性质即可得出；
（2）如图，以AC所在直线为x轴，以A为坐标原点，与AC垂直的直线为y轴，建立平面直角坐标系．由（1）知∠BAC=120°．（$\overrightarrow{PC}$+$\overrightarrow{PB}$）•$\overrightarrow{PA}$=2x²-x+$2{y}^{2}-2\sqrt{3}y$=$2[（x-\frac{1}{4}）^{2}+（y-\frac{\sqrt{3}}{2}）^{2}]$-$\frac{13}{8}$，即可得出．

解答 解：（1）∵|$\overrightarrow{a}$|=4，|$\overrightarrow{b}$|=3，（2$\overrightarrow{a}$-3$\overrightarrow{b}$）•（2$\overrightarrow{a}$+$\overrightarrow{b}$）=61，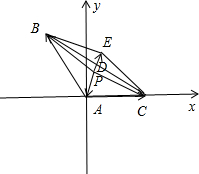
∴$4{\overrightarrow{a}}^{2}-3{\overrightarrow{b}}^{2}-4\overrightarrow{a}•\overrightarrow{b}=64-27-4\overrightarrow{a}•\overrightarrow{b}=61$；
∴$\overrightarrow{a}•\overrightarrow{b}=-6$；
∴$|\overrightarrow{a}+\overrightarrow{b}|=\sqrt{{\overrightarrow{a}}^{2}+2\overrightarrow{a}•\overrightarrow{b}+{\overrightarrow{b}}^{2}}$=$\sqrt{16-12+9}=\sqrt{13}$；
（2）如图，以AC所在直线为x轴，以A为坐标原点，与AC垂直的直线为y轴，建立平面直角坐标系．
由（1）知cos∠BAC=$\frac{\overrightarrow{a}•\overrightarrow{b}}{|\overrightarrow{a}||\overrightarrow{b}|}$=$\frac{-6}{4×3}$=-$\frac{1}{2}$；
∴∠BAC=120°．
则C（3，0），B$（-2，2\sqrt{3}）$，
设P（x，y），则$\overrightarrow{PB}$=$（-2-x，2\sqrt{3}-y）$，$\overrightarrow{PC}$=（3-x，-y），$\overrightarrow{PA}$=（-x，-y）．
∴（$\overrightarrow{PC}$+$\overrightarrow{PB}$）•$\overrightarrow{PA}$=2x²-x+$2{y}^{2}-2\sqrt{3}y$
=$2[（x-\frac{1}{4}）^{2}+（y-\frac{\sqrt{3}}{2}）^{2}]$-$\frac{13}{8}$≥$-\frac{13}{8}$，当且仅当取P$（\frac{1}{4}，\frac{\sqrt{3}}{2}）$取等号．
∴（$\overrightarrow{PC}$+$\overrightarrow{PB}$）•$\overrightarrow{PA}$的最小值为$-\frac{13}{8}$．

点评 本题考查了向量数量积运算性质、向量夹角公式、配方法，考查了推理能力与计算能力，属于中档题．