
分析 (1)利用绝对值不等式的解集,列出方程求解即可.
(2)利用a=1,若存在x∈R,使得不等式f(2x+1)-f(x-1)≤3-2m成立,化简函数的解析式,通过函数的最小值以及函数的单调性,列出不等式,求解即可.
解答 解:(1)显然a≠0,当a>0时,解集为:[$-\frac{1}{a}$,$\frac{3}{a}$],-$\frac{1}{a}=-3$,$\frac{3}{a}=1$,无解;
当a<0时,解集为:[$\frac{3}{a}$,-$\frac{1}{a}$],令-$\frac{1}{a}$=1,$\frac{3}{a}=-3$,解得a=-1,
综上a=-1.
(2)a=1时,令h(x)=f(2x+1)-f(x-1)=|2x|-|x-2|=$\left\{\begin{array}{l}{-x-1,x≤0}\\{3x-2,0<x≤2}\\{x+2,x>2}\end{array}\right.$,
由此可知,h(x)在(-∞,0],上是单调递减,
在[0,+∞)上单调递增,则x=0时,h(x)取得最小值-2,
由题意可知-2≤3-2m,则实数m的取值范围是(-∞,$\frac{5}{2}$].
点评 本题考查函数的最值的应用,绝对值不等式的解法,考查转化思想以及计算能力.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-ln2}{2}$ | B. | $\frac{3-2ln2}{4}$ | C. | $\frac{1+ln2}{2}$ | D. | $\frac{1+2ln2}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
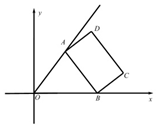 已知射线OP:y=$\frac{4}{3}$x(x≥0)和矩形ABCD,AB=16,AD=9,点A、B分别在射线OP和x轴非负半轴上,则线段OD长度的最大值为( )
已知射线OP:y=$\frac{4}{3}$x(x≥0)和矩形ABCD,AB=16,AD=9,点A、B分别在射线OP和x轴非负半轴上,则线段OD长度的最大值为( )| A. | $\sqrt{337}$ | B. | 27 | C. | $\sqrt{689}$ | D. | 29 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{2}}{2}$<x0<1 | B. | 1<x0<$\sqrt{2}$ | C. | $\sqrt{2}$<x0<$\sqrt{3}$ | D. | $\sqrt{3}$<x0<2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 30° | B. | $-\frac{3}{4}$ | C. | $\frac{{10\sqrt{3}}}{3}$ | D. | $5\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1,2} | B. | {1,2} | C. | {2,3} | D. | {0,2,3} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题

查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com