
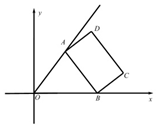
 已知射线OP:y=$\frac{4}{3}$x(x≥0)和矩形ABCD,AB=16,AD=9,点A、B分别在射线OP和x轴非负半轴上,则线段OD长度的最大值为( )
已知射线OP:y=$\frac{4}{3}$x(x≥0)和矩形ABCD,AB=16,AD=9,点A、B分别在射线OP和x轴非负半轴上,则线段OD长度的最大值为( )| A. | $\sqrt{337}$ | B. | 27 | C. | $\sqrt{689}$ | D. | 29 |
分析 通过设∠OBA=θ,并用角θ的三角函数值表示点D坐标,利用向量模的计算公式、结合三角函数有界性可得结论.
解答 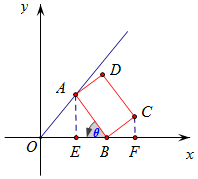 解:设∠OBA=θ,则∠CBx=$\frac{π}{2}$-θ,∠ABx=π-θ,如图,
解:设∠OBA=θ,则∠CBx=$\frac{π}{2}$-θ,∠ABx=π-θ,如图,
由题可知AE=16cosθ,AE=16sinθ,OE=$\frac{AE}{\frac{4}{3}}$=12sinθ,
BF=BCcos($\frac{π}{2}$-θ)=9sinθ,CF=BCsin($\frac{π}{2}$-θ)=9cosθ,
则A(12sinθ,16sinθ),B(16sinθ+16cosθ,0),C(25sinθ+16cosθ,9cosθ),
由四边形ABCD是矩形可知D(21sinθ,16sinθ+9cosθ),
因为$|\overrightarrow{OD}{|}^{2}$=441sin2θ+256sin2θ+288sinθcosθ+81cos2θ
=81(sin2θ+cos2θ)+308•2sin2θ+144sin2θ
=81+308•(1-cos2θ)+144sin2θ
=389+144sin2θ-308cos2θ
=389-340sin(2θ-φ)
≤389+340=729,
所以$|\overrightarrow{OD}|$≤27,
故选:B.
点评 本题考查函数最值及其几何意义,考查转化思想,涉及平面向量、三角恒等变换等基础知识,注意解题方法的积累,属于难题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | (-2,0]∪(2,+∞) | B. | (-2,+∞) | C. | (-∞,-2)∪(0,2) | D. | (-∞,2) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{30}$ | B. | -$\frac{13}{30}$ | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )
如图,已知A、B分别是函数f(x)=$\sqrt{3}$cos(ωx-$\frac{π}{2}$)(ω>0)在y轴右侧图象上的第一个最高点和第一个最低点,且∠AOB=$\frac{π}{2}$,则为了得到函数y=$\sqrt{3}$sin($\frac{π}{2}$x+$\frac{π}{3}$)的图象,只需把函数y=f(x)的图象( )| A. | 向左平行移动$\frac{π}{3}$个单位长度 | B. | 向左平行移动$\frac{1}{3}$个单位长度 | ||
| C. | 向左平行移动$\frac{2}{3}$个单位长度 | D. | 向左平行移动$\frac{2π}{3}$个单位长度 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ab<ac | B. | ba>ca | C. | logab<logac | D. | $\frac{a}{b}>\frac{a}{c}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com