
已知点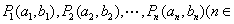
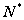
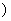 在函数
在函数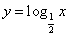 的图象上.
的图象上.
(1)若数列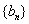 是等差数列,求证:数列
是等差数列,求证:数列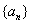 是等比数列;
是等比数列;
(2)若数列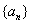 的前
的前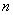 项和
项和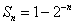 ,过点
,过点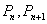 的直线与两坐标轴所围图形的面积为
的直线与两坐标轴所围图形的面积为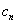 ,求最小的实数
,求最小的实数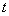 ,使得对任意的
,使得对任意的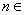
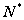 ,
,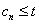 恒成立.
恒成立.
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:高中数学 来源: 题型:
已知下列命题:
①设m为直线,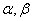 为平面,且m
为平面,且m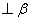 ,则“m//
,则“m//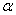 ”是“
”是“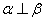 ”的充要条件;
”的充要条件;
②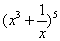 的展开式中含x3的项的系数为60;
的展开式中含x3的项的系数为60;
③设随机变量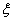 ~N(0,1),若P(
~N(0,1),若P(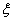 ≥2)=p,则P(-2<
≥2)=p,则P(-2<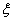 <0)=
<0)=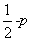 ;
;
④若不等式|x+3|+|x-2|≥2m+1恒成立,则m的取值范围是(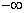 ,2);
,2);
⑤已知奇函数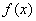 满足
满足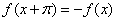 ,且0<x<
,且0<x<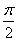 时
时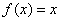 ,则函数
,则函数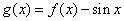 在[
在[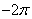 ,
,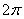 ]上有5个零点.
]上有5个零点.
其中所有真命题的序号是 ( )
A.③④ B.③ C.④⑤ D.②④
查看答案和解析>>
科目:高中数学 来源: 题型:
小赵和小王约定在早上7:00至7:30之间到某公交站搭乘公交车去上学.已知在这段时间内,共有3班公交车到达该站,到站的时间分别为7:10,7:20,7:30,如果他们约定见车就搭乘,则小赵和小王恰好能搭乘同一班公交车去上学的概率为 ( )
A.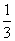 B.
B. 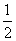 C.
C. 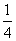 D.
D. 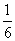
查看答案和解析>>
科目:高中数学 来源: 题型:
甲、乙两个一次射击比赛各射靶5次,两人成绩的条形统计图如图所示,则( )
A.甲的成绩的方差小于乙的成绩的方差
B.甲的成绩的平均数小于乙的成绩的平均数
C.甲的成绩的中位数小于乙的成绩的中位数
D.甲的成绩的极差小于乙的成绩的极差
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com