
| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ | D. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) |
分析 各项两式变形后,利用诱导公式化简,根据正弦与余弦函数的单调性即可做出判断.
解答 解:A,∵sin168°=sin(180°-12°)=sin12°,
又∵y=sinx在x∈[0,$\frac{π}{2}$]上是增函数,
∴sin11°<sin12°,即sin11°<sin168°.故错误;
B,∵sin194°=sin(180°+14°)=-sin14°,
cos160°=cos(180°-20°)=-cos20°=-sin70,
又∵y=sinx在x∈[0,$\frac{π}{2}$]上是增函数,
∴sin14°<sin70°,即cos160°<sin194°.故错误;
C,∵cos(-$\frac{15π}{8}$)=-cos$\frac{7π}{8}$,
cos$\frac{14π}{9}$=-cos$\frac{5π}{9}$,
又∵y=cosx在x∈[0,π]上是减函数,
∴-cos$\frac{5π}{9}$<-cos$\frac{7π}{8}$,即cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$.故正确;
D,∵tan(-$\frac{π}{5}$)=-tan$\frac{π}{5}$,
tan(-$\frac{3π}{7}$)=-tan$\frac{3π}{7}$,
又∵y=tanx在x∈[0,$\frac{π}{2}$]上是增函数,
∴tan$\frac{π}{5}$<tan$\frac{3π}{7}$,即tan(-$\frac{π}{5}$)>tan(-$\frac{3π}{7}$).故错误;
故选:C.
点评 此题考查了运用诱导公式化简求值,熟练掌握诱导公式,先转化再利用单调性比较大小是解本题的关键,考查了计算能力,属于中档题,


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-$\frac{2}{3}$,$\frac{2}{3}$] | B. | [-$\frac{1}{3}$,$\frac{1}{3}$] | C. | [0,$\frac{2}{3}$] | D. | [0,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1-2i | B. | -$\frac{1}{2}$+i | C. | -$\frac{1}{2}$-i | D. | $\frac{1}{2}$-i |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
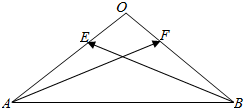 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com