
分析 (Ⅰ)根据幂的运算法则进行化简、计算即可;
(Ⅱ)由分母不为0,列出不等式求出解集即可,再计算g(2)与f(g(2))的值.
解答 解:(Ⅰ)$\root{3}{(-4)^{3}}$-($\frac{1}{2}$)0+25${\;}^{\frac{1}{2}}$=-4-1+5=0;
(Ⅱ)∵函数f(x)=$\frac{1}{1+x}$,
∴x+1≠0,
解得x≠-1,
∴函数f(x)的定义域为{x|x≠-1};
又g(x)=x2+2,
∴g(2)=22+2=6,
∴f(g(2))=f(6)=$\frac{1}{1+6}$=$\frac{1}{7}$.
点评 本题考查了根式与幂的运算法则的应用问题,也考查了求函数的定义域和计算函数值的应用问题,是基础题


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
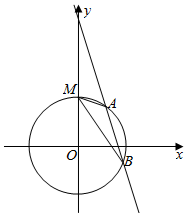 已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.
已知圆O:x2+y2=r2(r>0)与y轴的正半轴交于点M,直线l1:y=2x+1被圆O所截得的弦长为$\frac{4\sqrt{5}}{5}$,圆O上相异两动点A,B所在的直线l2的方程为y=kx+m,且满足直线MA与直线MB的斜率之积为$\frac{\sqrt{3}}{3}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | sin11°>sin168° | B. | sin194°<cos160° | ||
| C. | cos(-$\frac{15π}{8}$)>cos$\frac{14π}{9}$ | D. | tan(-$\frac{π}{5}$)<tan(-$\frac{3π}{7}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com