
分析 (Ⅰ)任取x1,x2∈[-1,1],且x1<x2,利用函数的单调性的定义证明f(x)在[-1,1]上单调递增.
(Ⅱ)利用f(x)在[-1,1]上单调递增,列出不等式组,即可求出不等式的解集.
(Ⅲ)问题转化为m2-2am≥0,对a∈[-1,1]恒成立,通过①若m=0,②若m≠0,分类讨论,判断求解即可.
解答 解:(Ⅰ)任取x1,x2∈[-1,1],且x1<x2,则-x2∈[-1,1],∵f(x)为奇函数,
∴f(x1)-f(x2)=f(x1)+f(-x2)=$\frac{f(x1)+f(-x2)}{x1+(-x2)}$•(x1-x2),…(2分)
由已知得$\frac{f(x1)+f(-x2)}{x1+(-x2)}$>0,x1-x2<0,∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴f(x)在[-1,1]上单调递增.…(4分)
(Ⅱ)∵f(x)在[-1,1]上单调递增,∴$\left\{\begin{array}{l}-1≤2x-1≤1\\-1≤1-3x≤1\\ 2x-1<1-3x\end{array}\right.$…(6分)
∴不等式的解集为$\left\{{\left.x\right|0≤x<\frac{2}{5}}\right\}$.…(7分)
(Ⅲ)∵f(1)=1,f(x)在[-1,1]上单调递增.∴在[-1,1]上,f(x)≤1.
问题转化为m2-2am+1≥1,即m2-2am≥0,对a∈[-1,1]恒成立.…(9分)
下面来求m的取值范围.设g(a)=-2m•a+m2≥0.
①若m=0,则g(a)=0≥0,对a∈[-1,1]恒成立.
②若m≠0,则g(a)为a的一次函数,若g(a)≥0,对a∈[-1,1]恒成立,
必须g(-1)≥0且g(1)≥0,∴m≤-2或m≥2.
综上,m=0 或m≤-2或m≥2…(12分)
点评 本题考查函数的单调性的判断与应用,函数恒成立的应用,考查计算能力.


 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
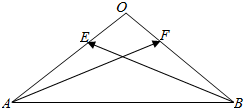 等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.
等腰△OAB中,∠A=∠B=30°,E、F分别是直线OA、OB上的动点,$\overrightarrow{OA}$、$\overrightarrow{OB}$上的动点,$\overrightarrow{OE}$=λ$\overrightarrow{OA}$,$\overrightarrow{OF}$=μ$\overrightarrow{OB}$,|$\overrightarrow{OA}$|=2,若$\overrightarrow{AE}$•$\overrightarrow{AB}$=9,则λ=-$\frac{1}{2}$;若λ+2μ=2,则$\overrightarrow{AF}$•$\overrightarrow{BE}$的最小值是-10.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
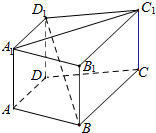 定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.
定义侧面与底面垂直的棱柱为直棱柱,在直四棱柱ABCD-A1B1C1D1中(如图),当底面四边形ABCD满足条件BD⊥AC时,有BD1⊥A1C1.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2+$\frac{{2\sqrt{6}}}{3}$ | B. | $\frac{{2\sqrt{6}}}{3}$ | C. | 1+$\frac{{2\sqrt{6}}}{3}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com