
| A. | $\sqrt{5}-2$ | B. | $2\sqrt{2}-1$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{6}-1$ |
分析 由设P(2cosα,$\sqrt{3}$sinα),则设$d=\sqrt{{x^2}+{y^2}+4y+4}-\frac{x}{2}$=$\sqrt{4co{s}^{2}α+3si{n}^{2}α+4\sqrt{3}sinα+4}$-cosα=$\sqrt{20-(sinα-2\sqrt{3})^{2}}$-cosα,当sinα=0,cosα=1时,d的最小值.
解答 解:椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$焦点在x轴上,由点P(x,y)在椭圆上,
设P(2cosα,$\sqrt{3}$sinα),则设$d=\sqrt{{x^2}+{y^2}+4y+4}-\frac{x}{2}$
=$\sqrt{4co{s}^{2}α+3si{n}^{2}α+4\sqrt{3}sinα+4}$-cosα,
=$\sqrt{20-(sinα-2\sqrt{3})^{2}}$-cosα,
当sinα=0,cosα=1时,
d的最小值为$d=\sqrt{{x^2}+{y^2}+4y+4}-\frac{x}{2}$=$\sqrt{20-12}$-1=2$\sqrt{2}$-1,
d的最小值2$\sqrt{2}$-1,
故选B.
点评 本题考查椭圆的参数方程,同角三角形函数的基本关系,考查三角函数的最值,考查计算能力,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:选择题
| A. | -6 | B. | -4 | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
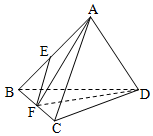 在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④
在正四面体ABCD中,点E,F分别是AB,BC的中点,则下列命题正确的序号是①③④查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com