
分析 (Ⅰ)求出首项,化简已知条件,利用等比数列的定义证明:数列{log3(1+an)}为等比数列;
(Ⅱ)求出首项的通项公式,然后求和,列出不等式求解即可.
解答 解:(Ⅰ)证明:由已知,${a_2}=a_1^2+2{a_1}=4{a_1}$,则a1(a1-2)=0,
因为数列{an}各项为正数,所以a1=2,
由已知,${a_{n+1}}+1={({{a_n}+1})^2}>0$,
得log3(an+1+1)=2log3(an+1).
又log3(a1+1)=log33=1,
所以,数列{log3(1+an)}是首项为1,公比为2的等比数列.…(6分)
(Ⅱ)由(Ⅰ)可知,${log_3}({1+{a_n}})={2^{n-1}}$,
所以${T_n}=1+2+{2^2}+…+{2^{n-1}}={2^n}-1$.
由Tn>520,得2n>521(n∈N*),
所以n≥10.
于是Tn>520成立时n的最小值为10.…(12分)
点评 本题考查等比数列的概念、等比数列通项公式与前n项和等基础知识,考查运算求解能力.


科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}-2$ | B. | $2\sqrt{2}-1$ | C. | $\sqrt{5}-1$ | D. | $\sqrt{6}-1$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[kπ-\frac{π}{12},kπ+\frac{5π}{12}](k∈Z)$ | B. | $[kπ+\frac{5π}{12},kπ+\frac{11π}{12}](k∈Z)$ | ||
| C. | $[kπ-\frac{5π}{24},kπ+\frac{7π}{24}](k∈Z)$ | D. | $[kπ+\frac{7π}{24},kπ+\frac{19π}{24}](k∈Z)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
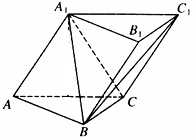 如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,
如图,三棱柱ABC-A1B1C1中,侧面AA1C1C⊥底面ABC,AA1=A1C=AC=2,AB=BC且AB⊥BC,查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{1}{2}$ | B. | 0 | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {0,1} | B. | {0,-1} | C. | {1,-1} | D. | {-1,0,1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ¬p:?x∈R,x2+x+1>0 | B. | ¬p:?x∈R,x2+x+1≠0 | ||
| C. | ¬p:?x∈R,x2+x+1≥0 | D. | ¬p:?x∈R,x2+x+1<0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com