
| A. | 向左平移$\frac{π}{8}$个单位得到 | B. | 向右平移$\frac{π}{8}$个单位得到 | ||
| C. | 向左平移$\frac{π}{4}$个单位得到 | D. | 向左右平移$\frac{π}{4}$个单位得到 |
分析 利用辅助角公式将函数化为同名函数进行比较即可.
解答 解:y=sin2x+cos2x=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
y=sin2x-cos2x=$\sqrt{2}$sin(2x-$\frac{π}{4}$)=$\sqrt{2}$sin[2(x-$\frac{π}{4}$)+$\frac{π}{4}$)],
∴由函数y=sin2x-cos2x的图象向左平移$\frac{π}{4}$个单位得到y=$\sqrt{2}$sin(2x+$\frac{π}{4}$),
故选:C.
点评 本题主要考查三角函数的图象关系,利用辅助角公式将函数化为同名函数是解决本题的关键.


 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
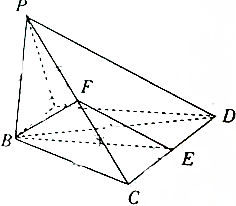 如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.
如图,在四棱锥P-ABCD中,AB⊥PA,AB∥CD,且PB=BC=BD=$\sqrt{6}$,CD=2AB=2$\sqrt{2}$,∠PAD=120°,E和F分别是侧棱CD和PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {m|m≠4} | B. | {m|m∈R} | C. | {m|m≤0} | D. | {m|m≤0或m≥4} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-2$\sqrt{5}$,2$\sqrt{5}$] | B. | [0,2] | C. | [-2$\sqrt{5}$,2] | D. | [$\frac{2\sqrt{5}}{5}$,1] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com