
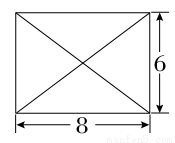
已知某几何体的俯视图是如图所示的矩形,正视图是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6,高为4的等腰三角形.
(1)求该几何体的体积V;
(2)求该几何体的侧面积S.
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案科目:高中数学 来源:2015高考数学(理)一轮配套特训:10-2排列与组合(解析版) 题型:选择题
在高三(1)班进行的演讲比赛中,共有5位选手参加,其中3位女生,2位男生.如果2位男生不能连续出场,且女生甲不能排在第一个,那么出场顺序的排法种数为( )
A.24 B.36 C.48 D.60
查看答案和解析>>
科目:高中数学 来源:2015高考数学(理)一轮考前特训:创新问题专项训练2(解析版) 题型:填空题
在平面直角坐标系xOy中,设点P(x1,y1),Q(x2,y2),定义:d(P,Q)=|x1-x2|+|y1-y2|.已知点B(1,0),点M为直线x-2y+2=0上的动点,则使d(B,M)取最小值时点M的坐标是________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:填空题
随机变量ξ的分布列如下
ξ | -1 | 0 | 1 |
P | a | b | c |
其中a,b,c成等差数列,若E(ξ)=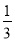 ,则D(ξ)=________.
,则D(ξ)=________.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理配套特训:10-9离散型随机变量均值方差和正态分布(解析版) 题型:选择题
已知随机变量X的分布列为
X | 1 | 2 | 3 |
P | 0.2 | 0.4 | 0.4 |
则E(6X+8)=( )
A.13.2 B.21.2 C.20.2 D.22.2
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:7-1空间几何体结构及三视图和直观图(解析版) 题型:选择题
已知某几何体的三视图如图所示,其中正(主)视图中半圆的半径为1,则该几何体的体积为( )
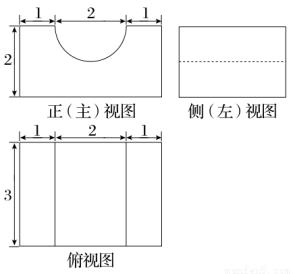
A.24-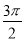 B.24-
B.24-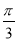
C.24-π D.24-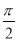
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:6-3二元一次不等式及简单的线性规划(解析版) 题型:解答题
为保增长、促发展,某地计划投资甲、乙两个项目,根据市场调研,知甲项目每投资100万元需要配套电能2万千瓦时,可提供就业岗位24个,GDP增长260万元;乙项目每投资100万元需要配套电能4万千瓦时,可提供就业岗位36个,GDP增长200万元.已知该地为甲、乙两个项目最多可投资3000万元,配套电能100万千瓦时,若要求两个项目能提供的就业岗位不少于840个,问如何安排甲、乙两个项目的投资额,才能使GDP增长的最多.
查看答案和解析>>
科目:高中数学 来源:2015高考数学理一轮配套特训:3-2同角三角函数基本关系式与诱导公式(解析版) 题型:选择题
△ABC是锐角三角形,若角θ终边上一点P的坐标为(sinA-cosB,cosA-sinC),则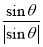 +
+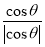 +
+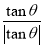 的值是( )
的值是( )
A.1 B.-1 C.3 D.4
查看答案和解析>>
科目:高中数学 来源:2015高考数学一轮配套特训:1-3简单的逻辑联结词全称量词与存在量词(解析版) 题型:选择题
下列说法中正确的是( )
A.“x>5”是“x>3”的必要不充分条件
B.命题“对?x∈R,恒有x2+1>0”的否定是“?x∈R,使得x2+1≤0”
C.?m∈R,使函数f(x)=x2+mx(x∈R)是奇函数
D.设p,q是简单命题,若p∨q是真命题,则p∧q也是真命题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com