
直线x=1与抛物线C:y2=4x交于M,N两点,点P是抛物线C准线上的一点,记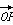 =a
=a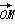 +b
+b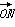 (a,b∈R),其中O为抛物线C的顶点.
(a,b∈R),其中O为抛物线C的顶点.
(1)当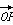 与
与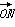 平行时,b=________;
平行时,b=________;
(2)给出下列问题:
①∀a,b∈R,△PMN不是等边三角形;
②∃a<0且b<0,使得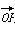 与
与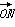 垂直;
垂直;
③无论点P在准线上如何运动,a+b=-1总成立.
其中,所有正确命题的序号是________.
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:
某体育用品商场经营一批每件进价为40元的运动服,先做了市场调查,得到数据如下表:
| 销售单价x(元) | 60 | 62 | 64 | 66 | 68 | … |
| 销售量y(件) | 600 | 580 | 560 | 540 | 520 | … |
根据表中数据,解答下列问题:
⑴ 建立一个恰当的函数模型,使它能较好地反映销售量y(件)与销售单价x(元)之间的函数关系,并写出这个函数模型的解析式 ;
;
⑵ 试求销售利润z(元)与销售单价x(元)之间的函数关系式(销售利润 = 总销售收入 - 总进价成本)并求价格为多少利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
在等比数列{an}中,a1=2,且an+1=an+2n.
(1)求数列{an}的通项an;
(2)数列{an}中是否存在这样的两项ap,aq(p<q),使得ap+aq=2 014?若存在,求符合条件的所有的p,q;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
复数z1,z2满足z1=m+(4-m2)i,z2=2cos θ+(λ+3sin θ)i(m,λ,θ∈R),并且z1=z2,则λ的取值范围是( )
A.[-1,1] B.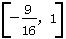
C.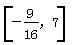 D.
D.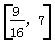
查看答案和解析>>
科目:高中数学 来源: 题型:
已知“整数对”按如下规律排成一列:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),…,则第60个“整数对”是( )
A.(7,5) B.(5,7)
C.(2,10) D.(10,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
图(1)是某地区参加2014年高考的学生身高的条形统计图,从左至右的各条形图表示的学生人数依次记为A1,A2,A3,…,A10(如A2表示身高(单位:cm)在[150,155)内的学生人数).图(2)是图(1)中统计身高在一定范围内学生人数的一个算法流程图.现要统计身高在[160,180)内的学生人数,那么流程图中判断框内整数k的值为________.
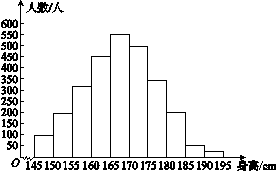
图(1)
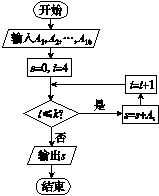
图(2)
查看答案和解析>>
科目:高中数学 来源: 题型:
已知数列{an}(n=1,2,3,…,2 012),圆C1:x2+y2-4x-4y=0和圆C2:x2+y2-2anx-2a2 013-ny=0,若圆C2平分圆C1的周长,则{an}的所有项的和为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
2013年12月21日上午10时,石家庄首次启动重污染天气Ⅱ级应急响应,正式实施机动车尾号限行,当天某报社为了解公众对“车辆限行”的态度,随机抽查了50人,将调查情况进行整理后制成下表:
| 年龄/岁 | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) | [65,75) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 赞成人数 | 4 | 6 | 9 | 6 | 3 | 4 |
(1)完成被调查人员的频率分布直方图;
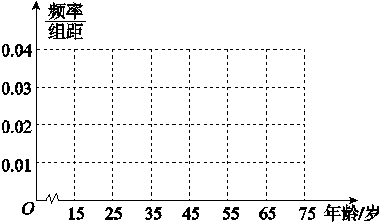
(2)若从年龄在[15,25),[25,35)的调查者中各随机选取两人进行追踪调查,记选中的4人中不赞成“车辆限行”的人数为ξ,求随机变量ξ的分布列和数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com