
| A. | {x|-2<x<-1,或x>3} | B. | {x|-3<x<-1,或x>2} | C. | {x|x<-3,或-1<x<2} | D. | {x|x<-3,或x>2} |
分析 根据分式不等式求解.$\frac{{x}^{2}+x-6}{x+1}$转化为$\left\{\begin{array}{l}{(x+1)({x}^{2}+x-6)>0}\\{x+1≠0}\end{array}\right.$,求根,利用穿根法求解即可.
解答 解:由题意:不等式$\frac{{x}^{2}+x-6}{x+1}$>0等价于(x+1)(x2+x-6)>0的解集,
利用穿根法求解:令(x+1)(x2+x-6)=0,
解得:x1=-1,x2=-3,x3=2.
将这三个根按从小到大顺序在数轴上标出来,如图: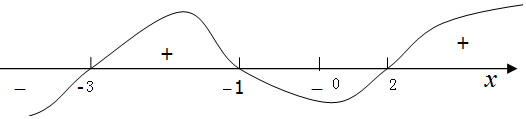
由图可看出不等式(x+1)(x2+x-6)>0的解集为{x|-3<x<-1或x>2}.
故选B.
点评 本题考查了高次不等式的解法,利用穿根法,要做到:“化正,求根,标轴,穿线(奇过偶不过),定解”.属于中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | C. | 奇函数或偶函数 | D. | 非奇非偶函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-2,0) | B. | (-2,2) | C. | (0,2) | D. | (-$\frac{1}{2}$,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1,-1 | B. | -1 | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com