Question

2．已知函数$f（x）=\left\{\begin{array}{l}2-|x|，x≤2\\{（{x-2}）^2}，x＞2\end{array}\right.$，函数$g（x）=\frac{b}{2}-f（2-x）$，其中b∈R，若函数y=f（x）-g（x）恰有4个零点，则b的取值范围是（　　）

• A． $（\frac{7}{8}，+∞）$
• B． $（\frac{7}{4}，2）$
• C． $（\frac{7}{8}，1）$
• D． $（\frac{7}{2}，4）$

Answer 1

分析 求出函数y=f（x）-g（x）的表达式，构造函数h（x）=f（x）+f（2-x），作出函数h（x）的图象，利用数形结合进行求解即可．

解答 解：∵g（x）=$\frac{b}{2}$-f（2-x），
∴y=f（x）-g（x）=f（x）-$\frac{b}{2}$+f（2-x），
由f（x）-$\frac{b}{2}$+f（2-x）=0，得f（x）+f（2-x）=$\frac{b}{2}$，
设h（x）=f（x）+f（2-x），
若x≤0，则-x≥0，2-x≥2，
则h（x）=f（x）+f（2-x）=2+x+x²，
若0≤x≤2，则-2≤-x≤0，0≤2-x≤2，
则h（x）=f（x）+f（2-x）=2-x+2-|2-x|=2-x+2-2+x=2，
若x＞2，-x＜-2，2-x＜0，
则h（x）=f（x）+f（2-x）=（x-2）²+2-|2-x|=x²-5x+8．
作出函数h（x）的图象如图：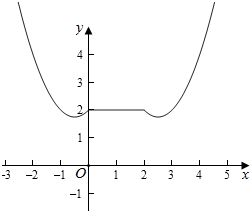

当x≤0时，h（x）=2+x+x²=（x+$\frac{1}{2}$）²+$\frac{7}{4}$≥$\frac{7}{4}$，
当x＞2时，h（x）=x²-5x+8=（x-$\frac{5}{2}$）²+$\frac{7}{4}$≥$\frac{7}{4}$，
故当$\frac{b}{2}$=$\frac{7}{4}$时，h（x）=$\frac{b}{2}$，有两个交点，
当$\frac{b}{2}$=2时，h（x）=$\frac{b}{2}$，有无数个交点，
由图象知要使函数y=f（x）-g（x）恰有4个零点，
即h（x）=$\frac{b}{2}$恰有4个根，
则满足$\frac{7}{4}$＜$\frac{b}{2}$＜2，解得：b∈（$\frac{7}{2}$，4），
故选：D．

点评 本题主要考查函数零点个数的判断，根据条件求出函数的解析式，利用数形结合是解决本题的关键．