
分析 根据函数的表达式可知函数f(x)为偶函数,判断函数在x大于零的单调性为递增,可得x2+$\frac{2}{3}$x+2>x2-x+1,解不等式即可.
解答 解:f(x)=2${\;}^{\sqrt{|x|+1}}$-$\frac{3}{1+{x}^{2}}$,定义域为R,
∵f(-x)=f(x),
∴函数f(x)为偶函数,
当x>0时,f(x)=2${\;}^{\sqrt{|x|+1}}$-$\frac{3}{1+{x}^{2}}$,函数单调递增,
根据偶函数性质可知:得f(x2+$\frac{2}{3}$x+2)>f(x2-x+1)成立,
∴x2+$\frac{2}{3}$x+2>x2-x+1
∴x>-$\frac{3}{5}$,
故答案为x>-$\frac{3}{5}$.
点评 考查了偶函数的性质和利用偶函数图象的特点解决实际问题,属于中档题.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:填空题
 传说古希腊毕达哥拉斯(Pythagoras,约公元前570年&公元前500年)学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数.根据下列四个图形及相应的正方形的个数的变化规律,第n个图形中有$\frac{n(n+1)}{2}$个正方形.
传说古希腊毕达哥拉斯(Pythagoras,约公元前570年&公元前500年)学派的数学家经常在沙滩上研究数学问题,他们在沙滩上画点或用小石子来表示数.根据下列四个图形及相应的正方形的个数的变化规律,第n个图形中有$\frac{n(n+1)}{2}$个正方形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
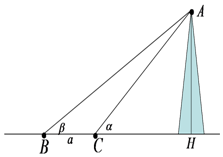 如图,在点B处测得山顶A的仰角为β,在点C处测得山顶A的仰角为α,BC=a,则山高AH为( )
如图,在点B处测得山顶A的仰角为β,在点C处测得山顶A的仰角为α,BC=a,则山高AH为( )| A. | $\frac{asinαsinβ}{{sin({α-β})}}$ | B. | $\frac{asinαcosβ}{{sin({α-β})}}$ | C. | $\frac{acosαsinβ}{{sin({α-β})}}$ | D. | $\frac{acosαcosβ}{{sin({α-β})}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | -2 | C. | -$\frac{1}{2}$ | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com