
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
分析 对用来衡量模拟效果好坏的几个量,即相关指数、残差平方和、相关系数及残差图中带状区域的宽窄进行分析,残差平方和越小越好,带状区域的宽度越窄,说明模型的拟合精度越高,R2越大,模型的拟合效果越好,模型的拟合效果越好,即可判断(1),(3);
利用正态曲线的性质,可判断(2)的正确性.
解答 解:用相关指数R2的值判断模型的拟合效果,R2越大,模型的拟合效果越好,故(1)正确;
正态分布N(μ,σ2)曲线中,μ一定时,σ越大,曲线越“矮胖”;σ越小,曲线越“瘦高”,表示取值越集中,故(2)不正确;
可用残差平方和判断模型的拟合效果,残差平方和越小,模型的拟合效果越好,故(3)正确.
故选:C.
点评 本题考查回归分析,本题解题的关键是理解对于拟合效果好坏的几个量的大小反映的拟合效果的好坏,同时考查考查正态曲线的性质,属于基础题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
 如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )
如图所示为某几何体的三视图,其中正视图和左视图都是腰长为1的等腰直角三角形,该几何体的体积为V1,其外接球的体积为V2,则$\frac{{V}_{2}}{{V}_{1}}$的值为( )| A. | $\sqrt{3}$π | B. | 2$\sqrt{3}$π | C. | 3$\sqrt{3}$π | D. | $\frac{3\sqrt{3}π}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | -2 | C. | $\frac{1}{2}$ | D. | -$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | $\frac{6}{7}$ | C. | $\frac{3}{10}$ | D. | $\frac{12}{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
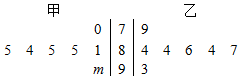
| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$ | B. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$ | ||
| C. | $\overline{{x}_{甲}}$=$\overline{{x}_{乙}}$ | D. | $\overline{{x}_{甲}}$,$\overline{{x}_{乙}}$的大小不确定 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | $\sqrt{2}$ | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com