
 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E1,F1分别是A1B1,C1D1的一个四等分点,
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点E1,F1分别是A1B1,C1D1的一个四等分点,分析 根据题图中的坐标系得到向量$\overrightarrow{B{E}_{1}},\overrightarrow{D{F}_{1}},\overrightarrow{{A}_{1}B},\overrightarrow{A{C}_{1}}$的坐标,利用向量的坐标运算解答.
解答 解:(1)由已知题图中坐标系得到D(0,0,0),B(1,1,0),E1(1,$\frac{3}{4}$,1),F1(0,$\frac{1}{4}$,1),
$\overrightarrow{B{E}_{1}}$=(0,$-\frac{1}{4}$,1),$\overrightarrow{D{F}_{1}}$=(0,$\frac{1}{4}$,1),
所以cos<$\overrightarrow{B{E}_{1}},\overrightarrow{D{F}_{1}}$>=$\frac{\overrightarrow{B{E}_{1}}•\overrightarrow{D{F}_{1}}}{|\overrightarrow{B{E}_{1}}||\overrightarrow{D{F}_{1}}|}$=$\frac{\frac{15}{16}}{\sqrt{\frac{17}{16}}\sqrt{\frac{17}{16}}}=\frac{15}{17}$,
所以BE1与DF1所成的角的余弦值为$\frac{15}{17}$;
(2)由(1)得$\overrightarrow{{A}_{1}B}$=(0,1,-1),$\overrightarrow{A{C}_{1}}$=(-1,1,1),
所以$\overrightarrow{{A}_{1}B}•\overrightarrow{A{C}_{1}}$=0,
所以$\overrightarrow{{A}_{1}B}⊥\overrightarrow{A{C}_{1}}$
所以1B⊥AC1.
点评 本题考查了正方体中线线关系的判断;解答本题的关键是利用空间向量的数量积.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
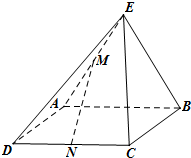 如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.
如图,矩形ABCD所在平面与直角三角形ABE所在平面互相垂直,AE⊥BE,点M,N分别是AE,CD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x2+(y+1)2=1 | B. | x2+(y+$\sqrt{3}$)2=3 | C. | x2+(y+$\frac{\sqrt{3}}{2}$)2=$\frac{3}{4}$ | D. | x2+(y+2)2=4 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图1,一个底面是正三角形,侧棱与底面垂直的棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图2,这时水面恰好为中截面(D,D′E,E′分别是棱CB,C′B′,CA,C′A′的中点),则图1中容器内水面的高度为$\frac{3}{2}$a.
如图1,一个底面是正三角形,侧棱与底面垂直的棱柱形容器,底面边长为a,高为2a,内装水若干.将容器放倒,把一个侧面作为底面,如图2,这时水面恰好为中截面(D,D′E,E′分别是棱CB,C′B′,CA,C′A′的中点),则图1中容器内水面的高度为$\frac{3}{2}$a.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.
如图,正方形ADEF与梯形ABCD所在的平面互相垂直,AD⊥CD,AB∥CD,AB=AD=2,CD=4,M为CE的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 既是奇函数,又是偶函数 | D. | 既非奇函数,又非偶函数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com