
| A. | $\frac{1}{3}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{5}{6}$ |
分析 根据面积比得出λ,μ的关系,用$\overrightarrow{AB},\overrightarrow{AC}$表示出$\overrightarrow{AG}$,从而可以$\overrightarrow{AP},\overrightarrow{AQ}$表示出$\overrightarrow{AG}$,利用共线原理列方程得出μ的值.
解答 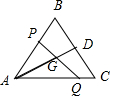 解:∵G是等边△ABC的重心,
解:∵G是等边△ABC的重心,
∴∠PAG=∠QAG=30°,
∵$\frac{{S}_{△PAG}}{{S}_{△QAG}}$=$\frac{\frac{1}{2}PA•GA•sin∠PAG}{\frac{1}{2}QA•GA•sin∠QAG}$=$\frac{2}{3}$,
∴$\frac{PA}{QA}=\frac{2}{3}$.
∵AB=AC,$\overrightarrow{AP}=λ\overrightarrow{AB}$,$\overrightarrow{AQ}=μ\overrightarrow{AC}$,
∴$\frac{λ}{μ}$=$\frac{2}{3}$,即λ=$\frac{2}{3}μ$.
∴$\overrightarrow{AB}$=$\frac{1}{λ}$$\overrightarrow{AP}$=$\frac{3}{2μ}$$\overrightarrow{AP}$,$\overrightarrow{AC}$=$\frac{1}{μ}$$\overrightarrow{AQ}$,
延长AG交BC于D,则D为BC的中点,
∴$\overrightarrow{AD}=\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$),
∵G是△ABC的重心,
∴$\overrightarrow{AG}$=$\frac{2}{3}$$\overrightarrow{AD}$=$\frac{2}{3}$×$\frac{1}{2}$($\overrightarrow{AB}+\overrightarrow{AC}$)=$\frac{1}{3}$$\overrightarrow{AB}+$$\frac{1}{3}\overrightarrow{AC}$=$\frac{1}{2μ}$$\overrightarrow{AP}$+$\frac{1}{3μ}$$\overrightarrow{AQ}$,
∵P,G,Q三点共线,
∴$\frac{1}{2μ}+\frac{1}{3μ}$=1,解得μ=$\frac{5}{6}$.
故选D.
点评 本题考查了平面向量的基本定理,共线定理,属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [2,+∞) | B. | (2,+∞) | C. | (0,2) | D. | (0,2] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知抛物线C:x2=2py(p>0)在点P(4,4)处的切线经过椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点E,椭圆C1的短轴长与抛物线C的焦距相等.
已知抛物线C:x2=2py(p>0)在点P(4,4)处的切线经过椭圆C1:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$的右焦点E,椭圆C1的短轴长与抛物线C的焦距相等.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 自2016年下半年起六安市区商品房价不断上涨,为了调查研究六安城区居民对六安商品房价格承受情况,寒假期间小明在六安市区不同小区分别对50户居民家庭进行了抽查,并统计出这50户家庭对商品房的承受价格(单位:元/平方),将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组(单位:元/平方),并作出频率分布直方图如图:
自2016年下半年起六安市区商品房价不断上涨,为了调查研究六安城区居民对六安商品房价格承受情况,寒假期间小明在六安市区不同小区分别对50户居民家庭进行了抽查,并统计出这50户家庭对商品房的承受价格(单位:元/平方),将收集的数据分成[0,2000],(2000,4000],(4000,6000],(6000,8000],(8000,10000]五组(单位:元/平方),并作出频率分布直方图如图:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com