
已知函数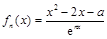 ,其中
,其中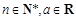 ,
,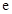 是自然对数的底数.
是自然对数的底数.
(1)求函数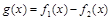 的零点;
的零点;
(2)若对任意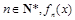 均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
均有两个极值点,一个在区间(1,4)内,另一个在区间[1,4]外,求a的取值范围;
(3)已知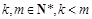 ,且函数
,且函数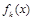 在R上是单调函数,探究函数
在R上是单调函数,探究函数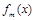 的单调性.
的单调性.
(1)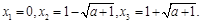 (2)
(2)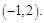 (3)函数
(3)函数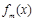 在R上是减函数
在R上是减函数
解析试题分析:(1)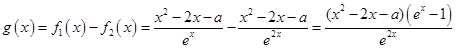
把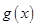 的零点问题转化为方程
的零点问题转化为方程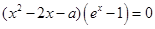 的根的问题.
的根的问题.
(2)因为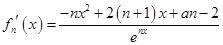 ,由题设可知
,由题设可知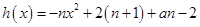 有两个两点,其中一个在
有两个两点,其中一个在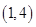 ,一个在
,一个在 外
外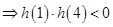 ,解这个不等式,可得实数
,解这个不等式,可得实数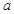 的取值范围.
的取值范围.
(3)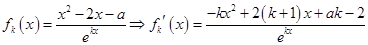
由函数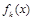 在R上是单调函数,所以
在R上是单调函数,所以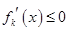 ,得到
,得到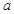 与
与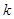 的关系,然后由此关系推出
的关系,然后由此关系推出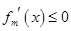 .
.
试题解析:
解:(1)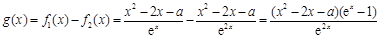 ,
,
令g(x)="0," 有ex-1=0,即x=0;或 x2-2x-a=0;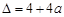 ,
,
①当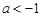 时,
时,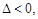 函数
函数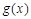 有1个零点
有1个零点 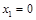 ; 1分
; 1分
②当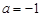 时,
时,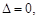 函数
函数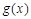 有2个零点
有2个零点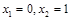 ;2分
;2分
③当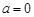 时,
时,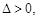 函数
函数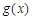 有两个零点
有两个零点 ;3分
;3分
④当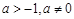 时,
时,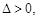 函数
函数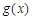 有三个零点:
有三个零点: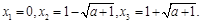 4分
4分
(2)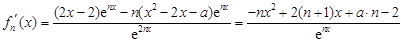 ,5分
,5分
设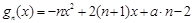 ,
,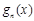 的图像是开口向下的抛物线,
的图像是开口向下的抛物线,
由题意对任意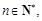
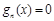 有两个不等实数根
有两个不等实数根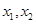 ,
,
且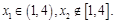 则对任意
则对任意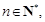
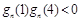 ,
,
即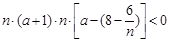 ,有
,有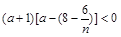 ,7分
,7分
又任意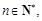
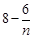 关于
关于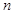 递增,
递增, 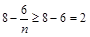 ,
,
故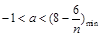 ,所以
,所以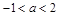 .
.
所以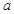 的取值范围是
的取值范围是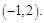 9分
9分
(3)由(2)知, 存在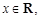
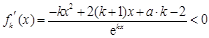 ,又函数
,又函数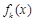 在R上是单调函数,故函数
在R上是单调函数,故函数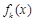 在R上是单调减函数, 10分
在R上是单调减函数, 10分
对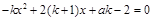 来说
来说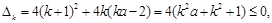 即
即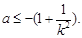 11分
11分
所以对于函数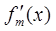 来说
来说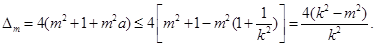
由 知
知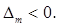 12分
12分
即对任意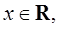
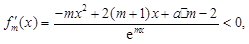
故函数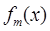 在R上是减函数. 13分
在R上是减函数. 13分
考点:1、函数的零点;2、利用导数研究函数的单调性;3、一元二次方程根的分布.


 举一反三期末百分冲刺卷系列答案
举一反三期末百分冲刺卷系列答案科目:高中数学 来源: 题型:解答题
设函数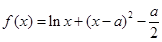 ,
,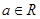 .
.
(1)若函数 在
在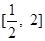 上单调递增,求实数
上单调递增,求实数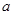 的取值范围;
的取值范围;
(2)求函数 的极值点.
的极值点.
(3)设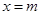 为函数
为函数 的极小值点,
的极小值点,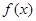 的图象与
的图象与 轴交于
轴交于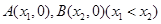 两点,且
两点,且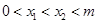 ,
,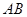 中点为
中点为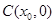 ,
,
求证: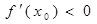 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
定义在定义域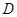 内的函数
内的函数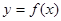 ,若对任意的
,若对任意的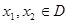 都有
都有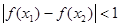 ,则称函数
,则称函数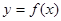 为“妈祖函数”,否则称“非妈祖函数”.试问函数
为“妈祖函数”,否则称“非妈祖函数”.试问函数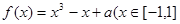 ,(
,(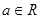 )是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
)是否为“妈祖函数”?如果是,请给出证明;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某建筑公司要在一块宽大的矩形地面(如图所示)上进行开发建设,阴影部分为一公共设施建设不能开发,且要求用栏栅隔开(栏栅要求在一直线上),公共设施边界为曲线f(x)=1-ax2(a>0)的一部分,栏栅与矩形区域的边界交于点M、N,交曲线于点P,设P(t,f(t)).
(1)将△OMN(O为坐标原点)的面积S表示成t的函数S(t);
(2)若在t= 处,S(t)取得最小值,求此时a的值及S(t)的最小值.
处,S(t)取得最小值,求此时a的值及S(t)的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com