
分析 由题意设燃放点的轨迹上的点M(x,y),由题意可得||MA|-|MB||=300×3=600<1000,然后利用双曲线的定义及方程得答案.
解答 解:以AB所在直线为x轴,AB的垂直平分线为y轴,建立坐标系,
则A(-500,0)、B(500,0),
设M(x,y)为曲线上任一点,
则||MA|-|MB||=300×2=600<1000.
∴a=300,c=500.
∴b2=c2-a2=(c+a)(c-a)=4002.
∴燃放点M的轨迹方程为$\frac{{x}^{2}}{30{0}^{2}}-\frac{{y}^{2}}{40{0}^{2}}=1$.
故答案为:$\frac{{x}^{2}}{30{0}^{2}}-\frac{{y}^{2}}{40{0}^{2}}=1$.
点评 本题考查了双曲线的定义及其标准方程,关键是对题意的理解,是中档题.


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源: 题型:选择题
| A. | α、β相交但不垂直 | B. | α⊥β | C. | α∥β | D. | 以上均不正确 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
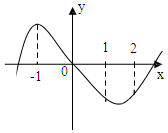
| A. | (-$\frac{3}{2}$,$\frac{1}{2}$ ) | B. | (-$\frac{2}{5}$,1) | C. | (-$\frac{1}{2}$,$\frac{3}{2}$) | D. | (-$\frac{3}{2}$,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
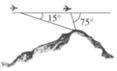 如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.
如图,飞机的航线和山顶在同一个铅垂平面内,已知飞机的高度为海拔15000 m,速度为1000 km/h,飞行员先看到山顶的俯角为15°,经过108s后又看到山顶的俯角为75°,则山顶的海拔高度为15-10$\sqrt{3}$km.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 模型1对应的r为-0.98 | B. | 模型2对应的r为0.80 | ||
| C. | 模型3对应的r为0.50 | D. | 模型4对应的r为-0.25 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
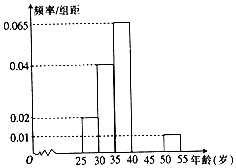 某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.
某市为评选“全国卫生城市”,从200名志愿者中随机抽取40名志愿者参加街道卫生监督活动,经过统计这些志愿者的年龄介于25岁和55岁之间,为方便安排任务,将所有志愿者按年龄从小到大分成六组,依次为[25,30),[30,35),[35,40),[40,45),[45,50),[50,55],如图是按照上述分组方法得到的频率分布直方图的一部分,已知第四组[40,45)的人数为4人.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [1,+∞) | B. | (0,1) | C. | (1,+∞) | D. | (-∞,1) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
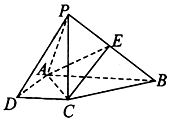 如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.
如图,在四棱锥P-ABCD中,四边形ABCD是直角梯形,AB⊥AD,AB∥CD,PC⊥底面ABCD,AB=2AD=2CD=4,PC=2a,E是PB的中点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com