
分析 根据题意得出k>$\frac{{x}_{0}(l{nx}_{0}+1)}{{x}_{0}-2}$,设f(x)=$\frac{x(lnx+1)}{x-2}$,其中x>2;利用导数求出f(x)在x>2的最小值,即可求出正整数k的最小值.
解答 解:?x0∈(2,+∞),∴x0-2>0,
∴k(x0-2)>x0(lnx0+1)可化为
k>$\frac{{x}_{0}(l{nx}_{0}+1)}{{x}_{0}-2}$,
设f(x)=$\frac{x(lnx+1)}{x-2}$,其中x>2;
则f′(x)=$\frac{[(lnx+1)+1](x-2)-x(lnx+1)}{{(x-2)}^{2}}$=$\frac{x-4-2lnx}{{(x-2)}^{2}}$;
令f′(x)=0,
得x-4-2lnx=0,
设g(x)=x-4-2lnx,其中x>2;
则g′(x)=1-$\frac{2}{x}$=$\frac{x-2}{x}$,
当x>2时,g′(x)>0,g(x)是单调增函数,
∴g(x)≥g(2);
且g(2)=2-4-2ln2=-2-2×0.6931<0,
g(5)=5-4-2ln5=1-2×1.6094<0,
g(8)=8-4-2ln8=4-6ln2=4-6×0.6931<0,
g(9)=9-4-2ln9=5-4ln3=5-4×1.0986>0;
∴g(x)在(8,9)内有零点,
且在零点处f(x)取得最小值m;
∴f(8)=$\frac{8(ln8+1)}{6}$=$\frac{4}{3}$×(3ln2+1)=$\frac{4}{3}$×(3×0.6931+1)≈4.1>m,
f(9)=$\frac{9(ln9+1)}{7}$=$\frac{9}{7}$×(2ln3+1)=$\frac{9}{7}$×(2×1.0986+1)≈4.1>m;
∴k≥4.1;
即正整数k的最小值为5.
故答案为:5.
点评 本题考查了特称命题的应用问题,也考查了不等式与函数的应用问题,是综合性题目.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{1}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{25}{4}$ | B. | $\frac{7}{4}$ | C. | -$\frac{9}{4}$ | D. | $\frac{41}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
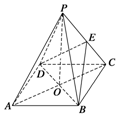 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{π}{2}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}-1}}{2}$ | B. | $\frac{{\sqrt{5}+1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{3+\sqrt{5}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
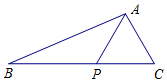 如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.
如图,在△ABC中,点P在BC边上,∠PAC=60°,PC=2,AP+AC=4.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 12π | C. | 20π | D. | 24π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ②③ | C. | ③④ | D. | ②④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com