
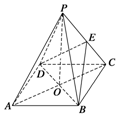
 如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.
如图所示,ABCD是正方形,O是正方形的中心,PO⊥底面ABCD,底面边长为a,E是PC的中点.分析 (1)连接OE,由中位线定理可知PA∥OE,故而PA∥面BDE;
(2)由BD⊥OP,BD⊥AC得出BD⊥平面PAC,从而得出平面PAC⊥平面BDE.
解答 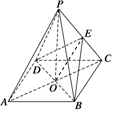 证明:(1)连接OE,
证明:(1)连接OE,
∵ABCD是正方形,O是正方形的中心,
∴O是AC的中点,又E是PC的中点,
∴OE∥PA,
又PA?平面BDE,OE?平面BDE,
∴PA∥面BDE.
(2)∵PO⊥底面ABCD,BD?平面ABCD,
∴PO⊥BD,
∵ABCD是正方形,
∴AC⊥BD,
又PO?平面PAC,AC?平面PAC,PO∩AC=O,
∴BD⊥平面PAC,
又BD?平面BDE,
∴平面PAC⊥平面BDE.
点评 本题考查了线面平行,线面垂直的判定,面面垂直的判定,属于基础题.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:选择题
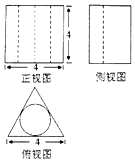
| A. | $16\sqrt{3}-\frac{16π}{3}$ | B. | $\frac{{16\sqrt{3}-16π}}{3}$ | C. | $8\sqrt{3}-\frac{8π}{3}$ | D. | $\frac{{8\sqrt{3}-8π}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:
我国古代数学典籍《九章算术》第七章“盈不足”中有一问题:| A. | T>2S? | B. | S>2T? | C. | S<2T? | D. | T<2S? |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $-\frac{5}{2}$ | B. | $-\frac{3}{2}$ | C. | -1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{3}$ | B. | $\frac{96}{125}$ | C. | $\frac{32}{81}$ | D. | $\frac{100}{243}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com