
���� ��4������ֱ�����жϣ����ɵó����ۣ�
��� �⣺����ΪAC=b=2��Ҫʹ�����������⣬����Ҫʹ��CΪԲ�ģ��뾶Ϊ2��Բ��BA���������㣬
��A=90��ʱԲ��AB���У���A=45��ʱ����B�㣬Ҳ����ֻ��һ�⣬
��45�㣼A��90�㣬��$\frac{\sqrt{2}}{2}$��sinA��1��
��b=2��B=45�㣬
�������Ҷ���a=x=$\frac{bsinA}{sinB}$=2$\sqrt{2}$sinA��
��$\frac{\sqrt{2}}{2}$��sinA��1��
��2$\sqrt{2}$sinA�ʣ�2��2$\sqrt{2}$����
��xȡֵ��Χ��2��x��2$\sqrt{2}$����ѡ����ȷ��
�ڡ�b=8��c=5��A=60�㣬
�������Ҷ����ã�a2=b2+c2-2bccosA=64+25-40=49��
��ã�a=7��
��������ABC�����Բ�뾶ΪR��
�������Ҷ����ã�2R=$\frac{7}{sin60��}$����ã�R=$\frac{7\sqrt{3}}{3}$����ѡ����ȷ��
�ۡ�AB=c=4��AC=b=7��BC=a=9��
�������Ҷ����ã�cosB=$\frac{2}{3}$��
��DΪBC���е㣬��BD=$\frac{1}{2}$BC=$\frac{9}{2}$��
��������ABD��AB=4��BD=$\frac{9}{2}$��cosB=$\frac{2}{3}$��
�����Ҷ����ã�AD2=AB2+BD2-2AB•BDcosB=$\frac{49}{4}$��
��ã�AD=$\frac{7}{2}$����ѡ����ȷ��
�ܡ�BC���ϵĸ�AD=BC=a��
��S��ABC=$\frac{1}{2}{a}^{2}=\frac{1}{2}bcsinA$��
��sinA=$\frac{{a}^{2}}{bc}$����cosA=$\frac{1}{2}$��$\frac{b}{c}$+$\frac{c}{b}$-$\frac{{a}^{2}}{bc}$����
��$\frac{b}{c}$+$\frac{c}{b}$=2cosA+sinA
=$\sqrt{5}$sin����+A����$\sqrt{5}$��
������sin��=$\frac{2\sqrt{5}}{5}$��cos��=$\frac{\sqrt{5}}{5}$����
��$\frac{b}{c}$+$\frac{c}{b}$��2��
��$\frac{b}{c}$+$\frac{c}{b}$��[2��$\sqrt{5}$]����ѡ����ȷ��
����ȷ˵��������Ǣ٢ڢۢܣ�
�ʴ�Ϊ���٢ڢۢܣ�
���� �������ڽ������ε����ͣ��漰��֪ʶ�У����ҡ����Ҷ��������Һ����Ķ�������ֵ�������ε������ʽ�������ǵ����Һ�����ʽ��ֱ������������Բ�뾶�����Ǻ��������Һ�����ʽ���Լ���������ʽ�����ã��������ն�������ʽ�ǽⱾ��Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $-\frac{4}{5}$ | B�� | $-\frac{1}{5}$ | C�� | $\frac{1}{5}$ | D�� | $\frac{4}{5}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
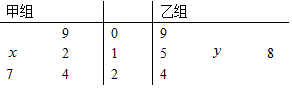 ��ͼ��Ҷͼ��¼�˼ף������������ѧ����һ��Ӣ�����������еijɼ�����λ���֣���֪�������ݵ���λ��Ϊ5���������ݵ�ƽ����Ϊ6.8����x��y��ֵ�ֱ�Ϊ��������
��ͼ��Ҷͼ��¼�˼ף������������ѧ����һ��Ӣ�����������еijɼ�����λ���֣���֪�������ݵ���λ��Ϊ5���������ݵ�ƽ����Ϊ6.8����x��y��ֵ�ֱ�Ϊ��������| A�� | 2��5 | B�� | 5��5 | C�� | 5��8 | D�� | 8��8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | K����СֵΪ1 | B�� | K����СֵΪ2 | C�� | K�����ֵΪ1 | D�� | K�����ֵΪ2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��c��b | C�� | c��a��b | D�� | b��c��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
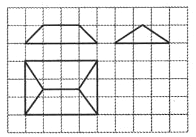 ���������������ҹ��Ŵ����ݼ�Ϊ�ḻ����ѧ�������������������⣺����ۻͯ���¹����ɣ������ɣ�������ɣ��㣬��һ�ɣ��ʣ������Σ�����˼��˵�������е���Ϊ���ε��ݼ�״Ш�壬�µ����3�ɣ���4�ɣ����ⳤ2�ɣ���һ�ɣ�����������Ƕ��٣�����֪һ��Ϊ10�ߣ��ֽ���Ш�������ͼ��������ͼ��ʾ����������ֽ��С�����εı߳�Ϊ1�����Ш������Ϊ��������
���������������ҹ��Ŵ����ݼ�Ϊ�ḻ����ѧ�������������������⣺����ۻͯ���¹����ɣ������ɣ�������ɣ��㣬��һ�ɣ��ʣ������Σ�����˼��˵�������е���Ϊ���ε��ݼ�״Ш�壬�µ����3�ɣ���4�ɣ����ⳤ2�ɣ���һ�ɣ�����������Ƕ��٣�����֪һ��Ϊ10�ߣ��ֽ���Ш�������ͼ��������ͼ��ʾ����������ֽ��С�����εı߳�Ϊ1�����Ш������Ϊ��������| A�� | 5000������ | B�� | 5500������ | C�� | 6000������ | D�� | 6500������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com