


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
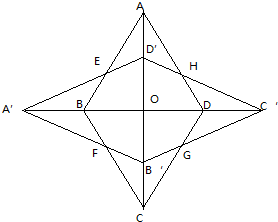 如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.
如图,菱形ABCD的对角线AC、BD相交于点O,AO=2BO=4,将菱形ABCD逆时针旋转90°得到菱形A′B′C′D′,求两个菱形重合部分的面积.查看答案和解析>>
科目:高中数学 来源: 题型:
| 种子处理 | 种子未处理 | 总计 | |
| 得病 | 32 | 101 | 133 |
| 不得病 | 61 | 213 | 274 |
| 总计 | 93 | 314 | 407 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| e1 |
| e2 |
| a |
| e1 |
| e2 |
| a |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| m |
| n |
| m |
| n |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、153π | B、160π |
| C、169π | D、360π |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com