
| A. | -5 | B. | 11 | C. | 15 | D. | 19 |
分析 先画出约束条件的可行域,利用目标函数Z=x+3y+7的几何意义求解最大值.
解答 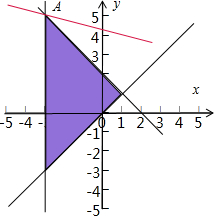 解:约束条件$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-y≤0}\\{x≥-3}\end{array}}\right.$的可行域如下图示:
解:约束条件$\left\{{\begin{array}{l}{x+y-2≤0}\\{x-y≤0}\\{x≥-3}\end{array}}\right.$的可行域如下图示:
由图易得目标函数z=x+3y+7在A处取得最大值,
由$\left\{\begin{array}{l}{x=-3}\\{x+y-2=0}\end{array}\right.$,解得A(-3,5)
z的最大值为:19.
故选:D.
点评 在解决线性规划的小题时,我们常用“角点法”,其步骤为:①由约束条件画出可行域⇒②求出可行域各个角点的坐标⇒③将坐标逐一代入目标函数⇒④验证,求出最优解.本题主要利用目标函数的几何意义求解.


科目:高中数学 来源: 题型:选择题
| A. | [-1,0] | B. | (-1,0) | C. | (-∞,0]∪[1,+∞) | D. | (-∞,-1)∪(0,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=x+3 | B. | f(x)=x-3 | C. | f(x)=2x+3 | D. | f(x)=2x-3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.
为了解中学生的身高情况,对某中学同龄的若干女生身高进行测量,将所得数据整理后,画出频率分布直方图如图所示.已知图中从左到右五个小组的频率分布为0.017,0.050,0.100,0.133,0.300,第三小组的频数为6.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
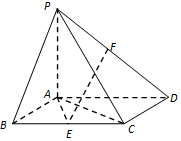 如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.
如图,已知四棱锥P-ABCD,底面ABCD为边长为2的菱形,PA⊥平面ABCD,∠ABC=60°,E是BC的中点,PA=AB.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com