
分析 (1)由角A可得$\overrightarrow{q}$的坐标,代入向量模的公式计算$|{\overrightarrow q}|$的值;
(2)由数量积的坐标运算得到$\overrightarrow{p}•\overrightarrow{q}$,利用辅助角公式化积,可得当A=$\frac{π}{3}$时,$\overrightarrow{p}•\overrightarrow{q}$取得最大值,求出对应的B值,再由正弦定理求得BC边的长.
解答 解:(1)当$A=\frac{π}{3}$时,$\overrightarrow{q}=(\frac{1+cosA}{2},sinA)=(\frac{3}{4},\frac{\sqrt{3}}{2})$,
∴$|\overrightarrow{q}|=\sqrt{(\frac{3}{4})^{2}+(\frac{\sqrt{3}}{2})^{2}}=\frac{\sqrt{21}}{4}$;
(2)$\overrightarrow{p}•\overrightarrow{q}=2•\frac{1+cosA}{2}+\sqrt{3}sinA$=$\sqrt{3}sinA+cosA+1=2sin(A+\frac{π}{6})+1$.
∴当A=$\frac{π}{3}$时,$\overrightarrow{p}•\overrightarrow{q}$取得最大值,此时B=$π-A-C=π-\frac{π}{3}-\frac{5π}{12}=\frac{π}{4}$,
根据正弦定理:$\frac{AC}{sinB}=\frac{BC}{sinA}$,得$BC=2\sqrt{3}×\frac{\sqrt{3}}{2}×\sqrt{2}=3\sqrt{2}$.
点评 本题考查平面向量的数量积运算,考查三角函数的图象和性质,是中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|0<x≤3} | B. | {x|1≤x≤3} | C. | {x|0≤x≤4} | D. | {x|1<x≤4} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{4}$ | B. | 2 | C. | $\frac{1}{2}$ | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | 11 | C. | 15 | D. | 19 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若a∥α,b∥α,则a∥b | B. | 若a∥α,b∥β,a∥b,则α∥β | ||
| C. | 若a⊥α,a?β,则α⊥β | D. | 若a,b在α内的射影相互垂直,则a⊥b |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
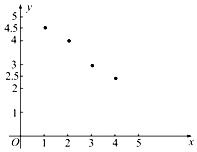 如表是某厂1~4月份用水量(单位:百吨)的一组数据.由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a,则a=( )
如表是某厂1~4月份用水量(单位:百吨)的一组数据.由散点图可知,用水量y与月份x之间有较好的线性相关关系,其线性回归方程是$\stackrel{∧}{y}$=-0.7x+a,则a=( )| 月份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
| A. | 10.5 | B. | 5.15 | C. | 5.2 | D. | 5.25 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com