
(2013·天津模拟)已知数列{an}的前n项和为Sn,且Sn=2an-2(n∈N*),数列{bn}满足b1=1,且点P(bn,bn+1)(n∈N*)在直线y=x+2上.
(1)求数列{an},{bn}的通项公式.
(2)求数列{an·bn}的前n项和Dn.
(3)设cn=an·sin2 -bn·cos2
-bn·cos2 (n∈N*),求数列{cn}的前2n项和T2n.
(n∈N*),求数列{cn}的前2n项和T2n.
(1)an=2an-1(n≥2) bn=2n-1
(2)Dn=(2n-3)2n+1+6
(3)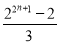 -2n2-n
-2n2-n
【解析】(1)当n=1时,a1=2,
当n≥2时,an=Sn-Sn-1=2an-2an-1,
所以an=2an-1(n≥2),所以{an}是等比数列,公比为2,首项a1=2,所以an=2n,
又点P(bn,bn+1)(n∈N*)在直线y=x+2上,所以bn+1=bn+2,
所以{bn}是等差数列,公差为2,首项b1=1,所以bn=2n-1.
(2)由(1)知an·bn=(2n-1)×2n,
所以Dn=1×21+3×22+5×23+7×24+…+(2n-3)×2n-1+(2n-1)×2n,①
2Dn=1×22+3×23+5×24+7×25+…+(2n-3)×2n+(2n-1)×2n+1.②
①-②得-Dn=1×21+2×22+2×23+2×24+…+2×2n-(2n-1)×2n+1
=2+2× -(2n-1)×2n+1
-(2n-1)×2n+1
=(3-2n)2n+1-6,
则Dn=(2n-3)2n+1+6.
(3)cn= ,
,
T2n=(a1+a3+…+a2n-1)-(b2+b4+…+b2n)
=2+23+…+22n-1-[3+7+…+(4n-1)]=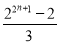 -2n2-n.
-2n2-n.


科目:高中数学 来源:2014年高考数学三轮冲刺模拟 集合、常用逻辑用语、不等式、函数与导数(解析版) 题型:选择题
若S1=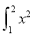 dx,S2=
dx,S2=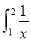 dx,S3=
dx,S3= dx,则S1,S2,S3的大小关系为( )
dx,则S1,S2,S3的大小关系为( )
A.S1<S2<S3 B.S2<S1<S3
C.S2<S3<S1 D.S3<S2<S1
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 立体几何(解析版) 题型:选择题
设三棱柱的侧棱垂直于底面,所有棱的长都为a,顶点都在一个球面上,则该球的表面积为( )
A.πa2 B.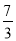 πa2 C.
πa2 C. πa2 D.5πa2
πa2 D.5πa2
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:填空题
已知x,y取值如下表:
x | 0 | 1 | 4 | 5 | 6 | 8 |
y | 1.3 | 1.8 | 5.6 | 6.1 | 7.4 | 9.3 |
从所得的散点图分析可知:y与x线性相关,且 =0.95x+a,则a=________.
=0.95x+a,则a=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 概率与统计(解析版) 题型:选择题
6位选手依次演讲,其中选手甲不在第一个也不在最后一个演讲,则不同的演讲次序共有( )
A.240种 B.360种 C.480种 D.720种
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:填空题
(2013·潍坊模拟)在△ABC中,角A,B,C所对的边分别为a,b,c,若acos B+bcos A=csin C,b2+c2-a2= bc,则角B=________.
bc,则角B=________.
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 数列、推理与证明(解析版) 题型:选择题
(2013·大纲全国卷)已知数列{an}满足3an+1+an=0,a2=-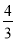 ,则{an}的前10项和等于( )
,则{an}的前10项和等于( )
A.-6(1-3-10) B. (1-3-10)
(1-3-10)
C.3(1-3-10) D.3(1+3-10)
查看答案和解析>>
科目:高中数学 来源:2014年高考数学三轮冲刺模拟 三角函数、解三角形与平面向量(解析版) 题型:选择题
已知函数f(x)=x3+ax2+bx+c,下列结论中错误的是( )
A.?x0∈R,f(x0)=0
B.函数y=f(x)的图象是中心对称图形
C.若x0是f(x)的极小值点,则f(x)在区间(-∞,x0)上单调递减
D.若x0是f(x)的极值点,则f′(x0)=0
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com