
分析 ①利用两角和差的正切公式进行化简即可,
②根据向量数量积与三角形夹角的关系进行判断,
③根据三角形重心的定义以及向量的基本运算进行判断,
④根据正弦定理进行判断,
⑤根据正弦定理,余弦定理以及三角形的面积公式进行判断即可.
解答 解:①若$α+β=\frac{7π}{4}$,则tan(α+β)=$\frac{tanα+tanβ}{1-tanαtanβ}$=-1,
即tanα+tanβ=tanα+tanβ-1,
则(1-tanα)•(1-tanβ)=1-(tanα+tanβ)+tanαtanβ=1-tanαtanβ+1+tanαtanβ=2;故①正确,
②已知$\overrightarrow{a}$=(1,-2),$\overrightarrow{b}$=(2,λ),且$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角,则$\overrightarrow{a}$•$\overrightarrow{b}$=2-2λ<0,则λ<1,
当$\overrightarrow{a}$与$\overrightarrow{b}$同向共线时,满足$\frac{2}{1}=\frac{λ}{-2}$,则λ=-4,则$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为锐角,则的实数λ的取值范围是λ<1且λ≠-4;故②错误,
③设BC的中点为D,则AD为△ABC中BC边上的中线,
∴$\overrightarrow{OP}=\overrightarrow{OA}+λ(\overrightarrow{AB}+\overrightarrow{AC})$=$\overrightarrow{OA}+2λ\overrightarrow{AD}$,
∴$\overrightarrow{AP}=2λ\overrightarrow{AD}$
∴P、A、D三点共线
∴P的轨迹一定通过△ABC的重心,故③正确,
④在△ABC中,∠A=60°,边长a,c分别为$a=4,c=3\sqrt{3}$,
则$\frac{a}{sinA}=\frac{c}{sinC}$,即sinC=$\frac{csinA}{a}$=$\frac{3\sqrt{3}×\frac{\sqrt{3}}{2}}{4}=\frac{9}{8}$>1,此时sinC不垂直,即△ABC没有解;故④错误,
⑤∵2R(sin2A-sin2C)=($\sqrt{2}$a-b)sinB,∴根据正弦定理,得a2-c2=($\sqrt{2}$a-b)b=$\sqrt{2}$ab-b2,
可得a2+b2-c2=$\sqrt{2}$ab
∴cosC=$\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}$=$\frac{\sqrt{2}ab}{2ab}$=$\frac{\sqrt{2}}{2}$,
∵角C为三角形的内角,∴角C的大小为$\frac{π}{4}$
∵c=2Rsin$\frac{π}{4}$=$\sqrt{2}$R
∴由余弦定理c2=a2+b2-2a•bcosC,可得
2R2=a2+b2-$\sqrt{2}$a•b≥2ab-$\sqrt{2}$ab=(2-$\sqrt{2}$)ab,当且仅当a=b时等号成立
∴ab≤$\frac{2{R}^{2}}{2-\sqrt{2}}$=($2+\sqrt{2}$)R2
∴S△ABC=$\frac{1}{2}$absinC≤$\frac{1}{2}$•($2+\sqrt{2}$)R2•$\frac{\sqrt{2}}{2}$=$\frac{1+\sqrt{2}}{2}$R2
即△ABC面积的最大值为$\frac{1+\sqrt{2}}{2}$R2;故⑤正确,
故答案为:①③⑤
点评 本题主要考查命题的真假判断,涉及两角和差的正切公式,向量的数量积以及基本运算,正弦定理和余弦定理的应用,综合性较强,难度较大.


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2) | C. | (1,1+$\sqrt{2}$) | D. | (2,2+$\sqrt{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | a、b、c都是奇数 | |
| B. | a、b、c都是偶数 | |
| C. | a、b、c中至少有两个奇数 | |
| D. | a、b、c中至少有两个奇数或都是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
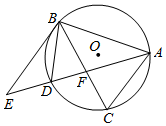 如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.
如图,△ABC内接于圆O,过B点的切线为BE,∠CBE的角平分线交圆O于点D,连接AD交BC于F,延长交BE于E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2i | B. | -2i | C. | -2 | D. | 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com