
分析 (Ⅰ)根据函数的奇偶性求出函数f(x)的解析式即可;
(Ⅱ)求出函数的导数,通过讨论a的范围,求出f(x)的最大值,得到关于a的方程,求出a的值并判断即可.
解答 解:(Ⅰ)设x∈(0,e],则-x∈[-e,0),∴f(-x)=-ax-lnx,
又f(x)为奇函数,f(x)=-f(-x)=ax+lnx.
∴函数f(x)的解析式为$f(x)=\left\{{\begin{array}{l}{ax-ln(-x),x∈[-e,0)}\\{ax+lnx,x∈(0,e]}\end{array}}\right.$…(4分)
(Ⅱ)假设存在实数a符合题意,则当x∈(0,e]时,f(x)的最大值是-3,
当x∈(0,e]时,${f^/}(x)=a+\frac{1}{x}=\frac{ax+1}{x}$,
①当a=0时,${f^/}(x)=a+\frac{1}{x}=\frac{ax+1}{x}>0$,
∴函数f(x)=ax+lnx是(0,e]上的增函数,
∴f(x)max=f(e)=ae+1=1,不合题意,舍去.
②当$-\frac{1}{a}<0⇒a>0$时,由于x∈(0,e].则${f^/}(x)=a+\frac{1}{x}>0$.
∴函数f(x)=ax+lnx是(0,e]上的增函数,
∴f(x)max=f(e)=ae+1=-3,则$a=-\frac{4}{e}$(舍去).
③当$0<-\frac{1}{a}<e⇒a<-\frac{1}{e}$时,
在$(0,-\frac{1}{a})$上f′(x)>0,在$(-\frac{1}{a},e]$上f′(x)<0.
则f(x)=ax+lnx在$(0,-\frac{1}{a})$上递增,$(-\frac{1}{a},e]$上递减,
∴$f{(x)_{max}}=f(-\frac{1}{a})=-1+ln(-\frac{1}{a})=-3$,解得a=-e2,
④当$e≤-\frac{1}{a}⇒-\frac{1}{e}≤a<0$时,由于x∈(0,e].则${f^/}(x)=a+\frac{1}{x}≥0$
∴函数f(x)=ax+lnx是(0,e]上的增函数,
∴f(x)max=f(e)=ae+1=-3,则$a=-\frac{4}{e}<-\frac{1}{e}$(舍去).
综上可知存在实数a=-e2,使得当x∈(0,e]时,f(x)的最大值是-3.…(12分)
点评 本题考查了函数的单调性、最值问题,考查导数的应用以及分类讨论思想,转化思想,是一道综合题.


 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案 启东小题作业本系列答案
启东小题作业本系列答案科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 2 | C. | 1 | D. | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x<3} | B. | {x|x≥5} | C. | {x|3≤x≤5} | D. | {x|3<x≤5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD
四棱锥E-ABCD中,△ABD为正三角形,∠BCD=120°,CB=CD-CE=1,AB=AD=AE=$\sqrt{3}$,且EC⊥BD查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | $\sqrt{2}$ | C. | 1 | D. | $\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{3\sqrt{2}}}{4}$ | B. | $\frac{9}{8}$ | C. | $\frac{{3\sqrt{5}}}{5}$ | D. | $\frac{{3\sqrt{2}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
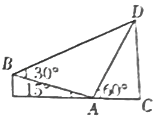 如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.
如图所示,在直角梯形BECD中,A为线段CE上一点,DC⊥EC,∠BAE=15°,∠DAC=60°,∠DBA=30°,AB=24m,则为CD=6$\sqrt{6}$m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com