
分析 (1)根据等比数列和等差数列通项公式,列方程即可求公差和公比,即可求得数列{an},{bn}的通项公式;
(2)由题意可知:求得log33n-1=n-1,根据等差数列前n项和公式,即可求得Sn.
解答 解:(1)由设等差的公差为d,首项a1,等比数列{bn}公比为q,首项为b1,
则a1=1,b1=1,$\left\{\begin{array}{l}{{a}_{1}+d={b}_{1}q}\\{2({a}_{1}+2d)-{b}_{1}{q}^{2}=1}\end{array}\right.$,
即$\left\{\begin{array}{l}{1+d=q}\\{2(1+2d)-{q}^{2}=1}\end{array}\right.$,整理得:$\left\{\begin{array}{l}{d=2}\\{q=3}\end{array}\right.$或$\left\{\begin{array}{l}{d=0}\\{q=1}\end{array}\right.$(舍去),
∴an=a1+(n-1)d=2n-1,bn=b1qn-1=3n-1,
∴数列{an}通项公式an=2n-1,{bn}的通项公式bn=3n-1;
(2)$log_3^{b_n}$=log33n-1=n-1,
则Sn=0+1+2+…+(n-1)=$\frac{n(n-1)}{2}$,
∴Sn=$\frac{n(n-1)}{2}$.
点评 本题考查等比数列及等差数列的通项公式,考查计算能力,属于中档题.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中数学 来源: 题型:解答题
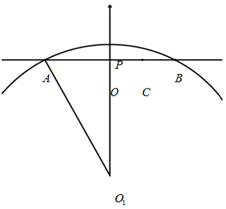 如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).
如图,某处立交桥为一段圆弧AB.已知地面上线段AB=40米,O为AB中点.桥上距离地面最高点P,且OP高5米.工程师在OB中点C处发现他的正上方桥体有裂缝.需临时找根直立柱,立于C处,用于支撑桥体.求直立柱的高度.(精确到0.01米).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 1+a1+a2 | C. | 2 | D. | 1+a1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若l∥α,α∩β=m,则l∥m | B. | 若l⊥α,l∥β,则α⊥β | ||
| C. | 若l∥m,m?α,则l∥α | D. | 若l∥α,m⊥l,则m⊥α |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?x∈R,f(x)≠f(x+T) | B. | ?x∈R,f(x)≠f(x+T) | C. | ?x∈R,f(x)=f(x+T) | D. | ?x∈R,f(x)=f(x+T) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com