
分析 (1)根据条件,利用互斥事件的概率公式,求该考生两年内可获得该职称的概率;
(2)确定X的取值,求出相应的概率,即可求X的分布列与数学期望.
解答 解:(1)设该考生两年内可获得该职称为事件A,则
P(A)=$\frac{1}{2}×\frac{1}{2}$+$\frac{1}{4}$×$\frac{2}{3}×\frac{2}{3}$+$\frac{1}{4}$×$\frac{3}{4}$×2=$\frac{53}{72}$;
(2)X的取值为2,3,4,则P(X=2)=$\frac{1}{4}$,P(X=3)=$\frac{1}{2}$,P(X=4)=$\frac{1}{4}$,
∴X的分布列为
| X | 2 | 3 | 4 |
| P | $\frac{1}{4}$ | $\frac{1}{2}$ | $\frac{1}{4}$ |
点评 本题考查相互独立事件的概率,考查离散型随机变量的期望与分布列,解题的关键是确定考生两年内参加考试的次数的含义.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{13}{18}$ | B. | $\frac{13}{22}$ | C. | $\frac{1}{6}$ | D. | $\frac{3}{22}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
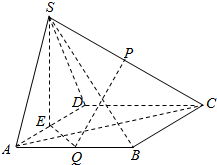 如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.
如图,在四棱锥S-ABCD中,底面ABCD为菱形,∠BAD=60°,平面SAD⊥平面ABCD,SA=SD,E,P,Q分别是棱AD,SC,AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3$\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2$\sqrt{3}$ | D. | 12 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0个 | B. | 至多有一个 | C. | 1个 | D. | 2个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com