
分析 由题意,通过的灯数X的取值分别为0、1、2、3、4,确定相应的概率,即可求出汽车停止前进时通过的信号灯数的分布列及期望.
解答 解:由题意,通过的灯数X的取值分别为0、1、2、3、4,
则P(X=0)=$\frac{1}{2}$,P(X=1)=$\frac{1}{4}$,P(X=2)=$\frac{1}{8}$,P(X=3)=P(X=4)=$\frac{1}{16}$,
∴X的分布列为
| X | 0 | 1 | 2 | 3 | 4 |
| P | $\frac{1}{2}$ | $\frac{1}{4}$ | $\frac{1}{8}$ | $\frac{1}{16}$ | $\frac{1}{16}$ |
点评 本题主要考查了相互独立事件的概率公式的应用,离散型随机变量的分布列及期望值的求解


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
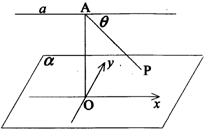 如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..
如图,已知直线a∥平面α,在平面α内有一动点P,点A是直线a上一定点,且AP与直线a所成角θ=$\frac{π}{4}$,点A到平面α的距离为2,若过点A作AO⊥α于点O,在平面α内,以过点O作直线a的平行线为x轴,以过点O作x轴的垂线为y轴建立直角坐标系,则动点P的轨迹方程为x2-y2=4..查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com