
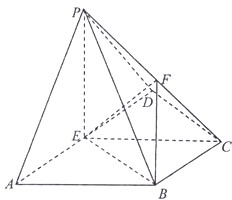
 如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,ABCD是梯形,BC∥AD,E,F分别是AD,PC的中点,△ABE,△BEC,△ECD都是边长为1的等边三角形.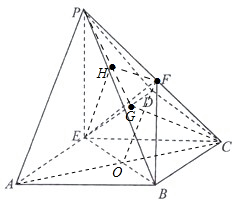 解:(1)证:连AC交EB与O,连OF
解:(1)证:连AC交EB与O,连OF | 1 |
| 2 |
| ||
| 4 |
| 1 |
| 2 |
| ||
| 4 |
| ||
| 4 |


 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案科目:高中数学 来源: 题型:
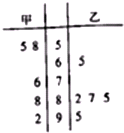 如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为
如图是甲、乙两名同学参加“汉字听写大赛”选拔性测试(在相同的测试条件下)5次测试的成绩(单位:分)的茎叶图,设甲乙两名同学的平均分数依次为. |
| x1 |
. |
| x2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
查看答案和解析>>
科目:高中数学 来源: 题型:
A、
| ||
| B、2 | ||
| C、3 | ||
| D、1 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| OA |
| OB |
| a |
| OM |
| OA |
| OB |
| 2 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| k |
| 1 |
| 2 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
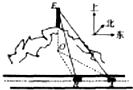 如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.
如图,一辆汽车在一条水平的公路上向正西方向行驶,在A处分别测得山顶上铁塔的塔顶E的仰角为θ和山脚点O(点O是点E在公路所在平面上的射影)的方位角是西偏北φ,再行驶akm到达B处,测得山脚点O的方位角是西偏北β.请设计一个方案,用测量的数据和有关公式写出计算OE的步骤.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com