
| A. | 3(3n-2n) | B. | 3n+2n | C. | 3n | D. | 3•2n-1 |
分析 直接利用且${S_n}=\frac{3}{2}({a_n}-1)(n∈{{N}^*})$,推出Sn-Sn-1=an,n≥2,得到数列{an}是以3为首项,以3为公比的等比数列.
解答 解:Sn为数列{an}的前n项和且 ${S_n}=\frac{3}{2}({a_n}-1)(n∈{{N}^*})$,所以an=Sn-Sn-1=$\frac{3}{2}$(an-1)-$\frac{3}{2}$(an-1-1),n≥2,
∴an=3an-1,n≥2,
∵S1=a1=$\frac{3}{2}$(a1-1),
∴a1=3,
∴数列{an}是以3为首项,以3为公比的等比数列,
∴an=3•3n-1=3n.
故选:C.
点评 本题是基础题,考查数列前n项和与通项公式的关系,等比数列的定义的应用,考查计算能力.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|x≤-2} | B. | {x|-2<x≤2} | C. | {x|-2≤x≤3} | D. | {x|-2≤x≤2} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
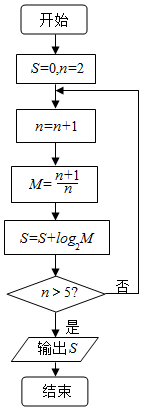
| A. | 1 | B. | log2$\frac{6}{5}$ | C. | log2$\frac{7}{3}$ | D. | log23 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com