
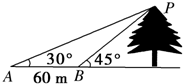
 如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度.
如图所示,为测一树的高度,在地面上选取A、B两点,从A、B两点分别测得树尖的仰角为30°,45°,且A、B两点之间的距离为60m,求树的高度. 分析 要求树的高度,需求PB长度,要求PB的长度,在△PAB由正弦定理可得.
解答 解:在△PAB,∠PAB=30°,∠APB=15°,AB=60,
sin15°=sin(45°-30°)=sin45°cos30°-cos45°sin30°=$\frac{\sqrt{6}-\sqrt{2}}{4}$,
由正弦定理得:PB=$\frac{ABsin30°}{sin15°}$=30($\sqrt{6}$+$\sqrt{2}$),
∴树的高度为PBsin45°=30×($\sqrt{6}$+$\sqrt{2}$)×$\frac{\sqrt{2}}{2}$=(30+30$\sqrt{3}$)m,
答:树的高度为(30+30$\sqrt{3}$)m.
点评 此题是实际应用题用到正弦定理和特殊角的三角函数值,正弦定理在解三角形时,用于下面两种情况:一是知两边一对角,二是知两角和一边,属中档题.


 全能练考卷系列答案
全能练考卷系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 两个程序输出结果相同 | |
| B. | 程序(1)输出的结果比程序(2)输出的结果大 | |
| C. | 程序(2)输出的结果比程序(1)输出的结果大 | |
| D. | 两个程序输出结果的大小不能确定,谁大谁小都有可能 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| P(K2≥x0) | 0.10 | 0.05 | 0.025 | 0.10 | 0.005 | 0.001 |
| x0 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com