
分析 (1)记G(x)=2x2-(4x-1)=2(x-1)2-1,x∈[0,2].利用二次函数的单调性可得|G(x)|的最大值为1,且G(0)=1,G(1)=-1,G(2)=1.
(2)F(x)=$\sqrt{x}$-(ax+b),由$\left\{\begin{array}{l}{-b=-M(a,b)}\\{2-(4a+b)=-M(a,b)}\end{array}\right.$,可得M(a,b)=b,a=$\frac{1}{2}$.存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,即可得出.
(3)M(a,b)=$\underset{max}{0≤x≤4}$$|\sqrt{x}-ax-b|$=$\underset{max}{0≤t≤2}$|t-at2-b|=$\left\{\begin{array}{l}{max\{|b|,|2-4a-b|,|\frac{1}{4a}-b|\},\frac{1}{2a}∈[0,2]}\\{max\{|b|,|2-4a-b|\},\frac{1}{2a}∉[0,2]}\end{array}\right.$.即可得出.
解答 解:(1)记G(x)=2x2-(4x-1)=2(x-1)2-1,x∈[0,2].则|G(x)|的最大值为1,
且G(0)=1,G(1)=-1,G(2)=1.故y=4x-1是g(x)=2x2,x∈[0,2]的“逼近函数”.
(2)F(x)=$\sqrt{x}$-(ax+b),由$\left\{\begin{array}{l}{-b=-M(a,b)}\\{2-(4a+b)=-M(a,b)}\end{array}\right.$,可得M(a,b)=b,a=$\frac{1}{2}$.
存在x0∈(0,4)满足F(x2)=M(a,b),即F(a,b)max=F(x2)=b,
即F(x)=$\sqrt{x}$-$\frac{1}{2}$x-b=-$\frac{1}{2}(\sqrt{x}-1)^{2}$+$\frac{1}{2}$-b,故x2=1.
由F(1)=$\frac{1}{2}$-b=b,可得b=$\frac{1}{4}$.
(3)证明:M(a,b)=$\underset{max}{0≤x≤4}$$|\sqrt{x}-ax-b|$=$\underset{max}{0≤t≤2}$|t-at2-b
|=$\left\{\begin{array}{l}{max\{|b|,|2-4a-b|,|\frac{1}{4a}-b|\},\frac{1}{2a}∈[0,2]}\\{max\{|b|,|2-4a-b|\},\frac{1}{2a}∉[0,2]}\end{array}\right.$.
当$\frac{1}{2a}$∉[0,2]时,2M(a,b)≥|b|+|2-4a-b|≥|2-4a|>1,故M(a,b)≥$\frac{1}{4}$.
点评 本题考查了二次函数的单调性、分类讨论方法、换元方法、绝对值的性质及其应用,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 8π | B. | 4π | C. | 2π | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
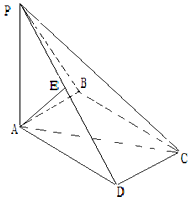 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,∠ABC=90°,四边形ABCD是平行四边形,且PA=AD=2,AB=1,E是线段PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
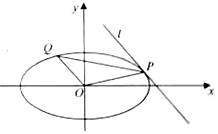 如图,P(x0,y0)是椭圆$\frac{{x}^{2}}{3}$+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方
如图,P(x0,y0)是椭圆$\frac{{x}^{2}}{3}$+y2=1的上的点,l是椭圆在点P处的切线,O是坐标原点,OQ∥l与椭圆的一个交点是Q,P,Q都在x轴上方查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com