
分析 (1)、(2)、(3)由诱导公式和同角三角函数关系化简.
(4)利用诱导公式,辅助角公式进行化简.
解答 解:(1)sin(-α)cos(-α-π)tan(2π+α)
=-sinα•(-cosα)•tanα
=sinαcosα•$\frac{sinα}{cosα}$
=-sin2α;
(2)$\frac{sin(180°+α)cos(-α)}{tan(-α)}$
=$\frac{-sinα•cosα}{-\frac{sinα}{cosα}}$
=cos2α;
(3)$\frac{cos(α+π)sin(-α)}{cos(-3π-α)sin(-α-4π)}$
=$\frac{cos(α+π)sin(-α)}{cos(α+π)sin(-α)}$
=1;
(4)sin2(-α)+tan(2π+α)cos2(π+α)
=sin2α+tanαcos2α
=sin2α+$\frac{sinα}{cosα}$•cos2α
=sin2α+sinαcosα
=sinα(sinα+cosα)
=$\sqrt{2}$sinαsin(α+$\frac{π}{4}$).
点评 本题主要考查了同角三角函数关系式、诱导公式以及辅助角公式的应用,考查计算能力.


科目:高中数学 来源: 题型:填空题
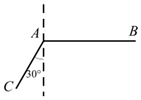 如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.
如图,当甲船位于A处时获悉,在其正东方向相距10海里的B处有个艘渔船遇险等待营救,甲船立即前往营救,同时把消息告知在甲船的南偏西30°,相距6海里的C处的乙船,乙船立即朝北偏东(θ+30°)的方向沿直线前往B处营救,则sinθ的值为$\frac{5\sqrt{3}}{14}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 57 | B. | 58 | C. | 62 | D. | 63 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | 3 | C. | 8 | D. | 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{12}$ | B. | $\frac{π}{8}$ | C. | $\frac{π}{6}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com