
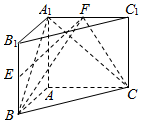
 如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.
如图,直三棱柱ABC-A1B1C1中,AB⊥AC,E,F分别是BB1,A1C1的中点.分析 (Ⅰ)可取CC1的中点M,并连接EM,FM,从而可以得到EM∥平面A1BC,FM∥平面A1BC,由面面平行的判定定理即可得出平面FEM∥平面A1BC,从而有EF∥平面A1BC;
(Ⅱ)根据条件可分别以AB,AC,AA1三直线为x,y,z轴,建立空间直角坐标系,可由AB=AC=AA1求出图形上一些点的坐标,从而得出$\overrightarrow{B{A}_{1}}=(-1,0,1),\overrightarrow{BC}=(-1,1,0),\overrightarrow{BF}=(-1,\frac{1}{2},1)$,可设平面A1BC的法向量为$\overrightarrow{{n}_{1}}=({x}_{1},{y}_{1},{z}_{1})$,根据$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{B{A}_{1}}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{BC}=0}\end{array}\right.$便可求出平面A1BC的一个法向量为$\overrightarrow{{n}_{1}}=(1,1,1)$,而同理可以求出平面FBC的一个法向量为$\overrightarrow{{n}_{2}}=(2,2,1)$,从而可以求出$cos<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>$,这便可得出二面角A1-BC-F的平面角的余弦值.
解答 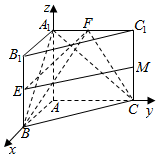 解:
解:
(Ⅰ)证明:如图,取CC1中点M,连结EM,FM;
∵E,F分别是BB1,A1C1的中点;
∴EM∥BC,FM∥A1C;
∴EM∥平面A1BC,FM∥平面A1BC,且EM∩FM=M;
∴平面EFM∥平面A1BC;
∴EF∥平面A1BC;
(Ⅱ)根据题意知,AB,AC,AA1三直线两两垂直,分别以这三直线为x,y,z轴,建立如图空间直角坐标系A-xyz,则:
B(1,0,0),C(0,1,0),A1(0,0,1),$F(0,\frac{1}{2},1)$;
∴$\overrightarrow{B{A}_{1}}=(-1,0,1),\overrightarrow{BC}=(-1,1,0)$,$\overrightarrow{BF}=(-1,\frac{1}{2},1)$;
设平面A1BC的法向量$\overrightarrow{{n}_{1}}$=(x1,y1,z1),则:
$\left\{\begin{array}{l}{\overrightarrow{{n}_{1}}•\overrightarrow{B{A}_{1}}=-{x}_{1}+{z}_{1}=0}\\{\overrightarrow{{n}_{1}}•\overrightarrow{BC}=-{x}_{1}+{y}_{1}=0}\end{array}\right.$,取x1=1,得y1=1,z1=1,∴$\overrightarrow{{n}_{1}}=(1,1,1)$;
同理可得平面FBC的一个法向量$\overrightarrow{{n}_{2}}=(2,2,1)$;
∴$cos<\overrightarrow{{n}_{1}},\overrightarrow{{n}_{2}}>=\frac{\overrightarrow{{n}_{1}}•\overrightarrow{{n}_{2}}}{|\overrightarrow{{n}_{1}}||\overrightarrow{{n}_{2}}|}=\frac{5}{\sqrt{3}•3}$=$\frac{5\sqrt{3}}{9}$;
所以二面角A1-BC-F的余弦值为$\frac{{5\sqrt{3}}}{9}$.
点评 考查三角形中位线的性质,线面平行及面面平行的判定定理,面面平行的性质,以及通过建立空间直角坐标系,利用空间向量解决几何问题的方法,能求空间点的坐标,平面法向量的概念及求法,以及向量夹角余弦的坐标公式.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:高中数学 来源: 题型:解答题
 如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.
如图,在等腰直角三角形ABC,∠C=90°,点D在线段AB上,且AD=$\frac{1}{3}$AB,延长线段CD至点E,使DE=CD,求cos∠CBE.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
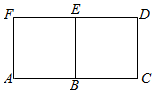 如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:
如图,矩形ACDF中,AC=2CD,B,E分别为AC,DF的中点,写出:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
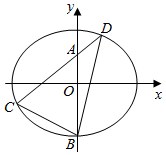 如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.
如图,椭圆E:$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{{\sqrt{3}}}{3}$,点$(\sqrt{3},\sqrt{2})$为椭圆上的一点.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{3}$ | B. | $\frac{1}{4}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
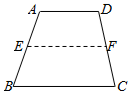 如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.
如图,梯形ABCD中,点E、F分别在AB、CD上,EF∥AD,假设EF作上下平行移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com